题目内容
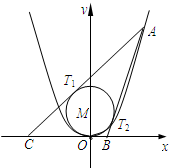 已知A是抛物线y=
已知A是抛物线y=| 1 |
| 4 |
(Ⅰ)证明:
| 1 |
| m |
| 1 |
| n |
(Ⅱ)已知点A在第一象限,且当△ABC周长最小时,试求△ABC的外接圆方程.
分析:(Ⅰ)设A(x,y),则n=
=y,所以2=r=
=
=
,由此能证明
+
为定值.
(Ⅱ)周长l=2(m+n).由
=
+
≥
≥
,知m+n≥16,l≥32,取最小值时,m=n=8,点A(4
,8).
设点B的横坐标为x0,则直线AB的方程为l:x=
y+x0,点M到l的距离2=
,由此及彼能得到所求的方程.
| x2+(y-2)2-22 |
| S△ABC |
| m+n |
| ||
| m+n |
| ||
| m+n |
| 1 |
| m |
| 1 |
| n |
(Ⅱ)周长l=2(m+n).由
| 1 |
| 4 |
| 1 |
| m |
| 1 |
| n |
| 2 | ||
|
| 4 |
| m+n |
| 2 |
设点B的横坐标为x0,则直线AB的方程为l:x=
4
| ||
| 8 |
|2(x0-4
| ||||
|
解答: (本小题满分16分)
(本小题满分16分)
解:(Ⅰ)设A(x,y),则n=
=y,
∴2=r=
=
=
,∴
+
=
.
(Ⅱ)周长l=2(m+n).
∵
=
+
≥
≥
,∴m+n≥16,∴l≥32,
取最小值时,m=n=8,点A的坐标为(4
,8).
设点B的横坐标为x0,则直线AB的方程为l:x=
y+x0,
即8x+(x0-4
)y-8x0=0.
点M到l的距离2=
,整理得
+4
x0-8=0.
故可设所求圆方程为:x2+y2+4
x+Ey-8=0,将点(4
,8)代入得E=-15,
∴所求的方程为:x2+y2+4
x-15y-8=0.
 (本小题满分16分)
(本小题满分16分)解:(Ⅰ)设A(x,y),则n=
| x2+(y-2)2-22 |
∴2=r=
| S△ABC |
| m+n |
| ||
| m+n |
| ||
| m+n |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 4 |
(Ⅱ)周长l=2(m+n).
∵
| 1 |
| 4 |
| 1 |
| m |
| 1 |
| n |
| 2 | ||
|
| 4 |
| m+n |
取最小值时,m=n=8,点A的坐标为(4
| 2 |
设点B的横坐标为x0,则直线AB的方程为l:x=
4
| ||
| 8 |
即8x+(x0-4
| 2 |
点M到l的距离2=
|2(x0-4
| ||||
|
| x | 2 0 |
| 2 |
故可设所求圆方程为:x2+y2+4
| 2 |
| 2 |
∴所求的方程为:x2+y2+4
| 2 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
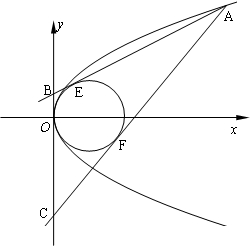 已知A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于E、F两点,交y轴于B、C两点.
已知A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于E、F两点,交y轴于B、C两点.