题目内容
在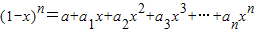 中,若2a2+an-5=0,则自然数n的值是( )
中,若2a2+an-5=0,则自然数n的值是( )A.7
B.8
C.9
D.10
【答案】分析:由二项展开式的通项公式Tr+1=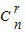 •(-1)rxr可得an=(-1)r•
•(-1)rxr可得an=(-1)r•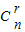 ,于是有2(-1)2
,于是有2(-1)2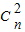 +(-1)n-5
+(-1)n-5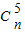 =0,由此可解得自然数n的值.
=0,由此可解得自然数n的值.
解答:解:由题意得,该二项展开式的通项公式Tr+1=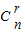 •(-1)rxr,
•(-1)rxr,
∴其二项式系数an=(-1)r•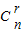 ,
,
∵2a2+an-5=0,
∴2(-1)2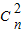 +(-1)n-5
+(-1)n-5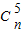 =0,即2
=0,即2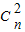 +(-1)n-5
+(-1)n-5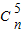 =0,
=0,
∴n-5为奇数,
∴2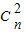 =
=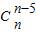 =
=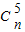 ,
,
∴2×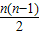 =
=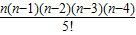 ,
,
∴(n-2)(n-3)(n-4)=120.
∴n=8.
故答案为:8.
点评:本体考察二项式定理的应用,着重考察二项式系数的概念与应用,由二项展开式的通项公式得到二项式系数an=(-1)r•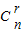 是关键,属于中档题.
是关键,属于中档题.
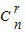 •(-1)rxr可得an=(-1)r•
•(-1)rxr可得an=(-1)r•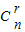 ,于是有2(-1)2
,于是有2(-1)2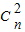 +(-1)n-5
+(-1)n-5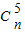 =0,由此可解得自然数n的值.
=0,由此可解得自然数n的值.解答:解:由题意得,该二项展开式的通项公式Tr+1=
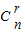 •(-1)rxr,
•(-1)rxr,∴其二项式系数an=(-1)r•
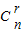 ,
,∵2a2+an-5=0,
∴2(-1)2
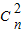 +(-1)n-5
+(-1)n-5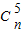 =0,即2
=0,即2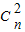 +(-1)n-5
+(-1)n-5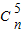 =0,
=0,∴n-5为奇数,
∴2
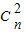 =
=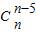 =
=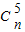 ,
,∴2×
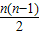 =
=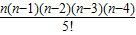 ,
,∴(n-2)(n-3)(n-4)=120.
∴n=8.
故答案为:8.
点评:本体考察二项式定理的应用,着重考察二项式系数的概念与应用,由二项展开式的通项公式得到二项式系数an=(-1)r•
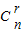 是关键,属于中档题.
是关键,属于中档题. 
练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 中,若2a2+an-5=0,则自然数n的值是( )
中,若2a2+an-5=0,则自然数n的值是( )