题目内容
(本小题满分12分)
向量
(1)若a为任意实数,求g(x)的最小正周期;
(2)若g(x)在[o, )上的最大值与最小值之和为7,求a的值,
)上的最大值与最小值之和为7,求a的值,
(1) (2)
(2)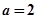
解析试题分析:g(x)=m·n=a+1+4sinxcos(x+ )
)
= sin2x-2sin2x+a+1=
sin2x-2sin2x+a+1= sin2x+cos2x+a=2sin(2x+
sin2x+cos2x+a=2sin(2x+ )+a (4分)
)+a (4分)
(1)g(x)=2sin(2x+ )+a,T=π. (6分)
)+a,T=π. (6分)
(2)∵0≤x< ,∴
,∴ ≤2x+
≤2x+ <
<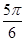
当2x+ =
=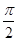 ,即x=
,即x= 时,ymax=2+a. (8分)
时,ymax=2+a. (8分)
当2x+ =
= ,即x=0时,ymin=1+a, (10分)
,即x=0时,ymin=1+a, (10分)
故a+1+2+a=7,即a=2. (12分)
考点:向量数量积及三角函数化简性质
点评:此类题目要求学生熟记三角公式,如诱导公式,二倍角公式,两角和差的正余弦公式,三角函数单调区间等,本题属于中档题

练习册系列答案
相关题目
设  为单位向量,若
为单位向量,若 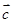 满足
满足 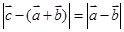 ,则
,则  的最大值为
的最大值为
A. | B.2 | C. | D.1 |
记 ,
, ,设
,设 为平面向量,则( )
为平面向量,则( )
A. |
B. |
C. |
D. |
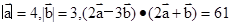 ,
, 的值;
的值; 的夹角
的夹角 ;
;  的值.
的值.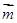 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量 =(2,0)所成角为
=(2,0)所成角为 ,其中A、B、C是△ABC的内角。
,其中A、B、C是△ABC的内角。 上的三点,向量
上的三点,向量 ﹑
﹑ ﹑
﹑ 满足:
满足: ]·
]· ;
; ;
; 时,x
时,x
 及b
及b 与
与 ,其中
,其中 。
。 若
若 ,求
,求 和
和 的值;
的值; 若
若 ,求
,求 的值域。
的值域。 .
.  三点共线,求实数
三点共线,求实数 的值;
的值;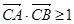 成立
成立 ,令
,令
 的周期为
的周期为 .
. 的解析式;
的解析式; 时
时 ,求实数
,求实数 的取值范围.
的取值范围.