题目内容
已知向量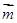 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量 =(2,0)所成角为
=(2,0)所成角为 ,其中A、B、C是△ABC的内角。
,其中A、B、C是△ABC的内角。
(1)求角B的大小;
(2)求sinA+sinC的取值范围。
(1)B= ,(2)
,(2)
解析试题分析:(1)由题知,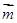 ×
× =(sinB,1-cosB)×(2,0)=2sinB, (2分)
=(sinB,1-cosB)×(2,0)=2sinB, (2分)
由数量积定义知,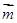 ×
× =ô
=ô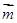 ô×ô
ô×ô ôcos
ôcos =
= ×2×
×2× =
= 4分)
4分)
∴4sin2B=2-2cosB,2cos2B-cosB-1=0,∴cosB=- ,B=
,B= ,cosB=1(舍去) (6分)
,cosB=1(舍去) (6分)
(2)由(1)可得:

考点:本题考查了数量积的运算及三角函数的性质
点评:此类问题比较综合,除了要求学生掌握数量积的坐标运算,还需掌握三角恒等变换公式及三角函数的性质、值域等知识

练习册系列答案
相关题目
设向量 ,若
,若 (
(
 ),则
),则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
 ,且
,且 ,求:
,求: 的坐标
的坐标 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角
 与
与 平行,求实数
平行,求实数 的值.
的值. ,其中
,其中 ,且
,且 .
. 交于两点M,N,且以MN为直径的圆过原点,求证:
交于两点M,N,且以MN为直径的圆过原点,求证: 为定值;
为定值; ,求椭圆长轴长的取值范围。
,求椭圆长轴长的取值范围。 =
= ,
,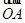 =
= ,
, =
=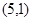 ,设
,设 是直线
是直线 上一点,
上一点, 是坐标原点
是坐标原点 取最小值时的
取最小值时的 ;
;  的余弦值。
的余弦值。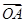 ,
, 为两个不共线向量。
为两个不共线向量。 ,求使
,求使 三个向量的终点在同一条直线上的
三个向量的终点在同一条直线上的 的值。
的值。
 )上的最大值与最小值之和为7,求a的值,
)上的最大值与最小值之和为7,求a的值,