题目内容
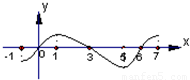
 设定义在[-1,7]上的函数y=f(x)的图象如图示,则关于函数
设定义在[-1,7]上的函数y=f(x)的图象如图示,则关于函数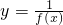 的单调区间表述正确的是
的单调区间表述正确的是
- A.在[-1,1]上单调递减
- B.在(0,1]上单调递减,在[1,3)上单调递增
- C.在[5,7]上单调递减
- D.在[3,5]上单调递增
B
分析:当x=0,x=3,x=6时,函数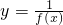 无意义,故排除A、C、D,进而可得答案.
无意义,故排除A、C、D,进而可得答案.
解答:由图象可知当x=0,x=3,x=6时,f(x)=0,
此时函数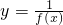 无意义,而选项A、C、D均违背定义域,
无意义,而选项A、C、D均违背定义域,
故排除A、C、D,
故选B.
点评:本题考查函数单调性的判断,涉及函数的定义的应用,属基础题.
分析:当x=0,x=3,x=6时,函数
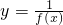 无意义,故排除A、C、D,进而可得答案.
无意义,故排除A、C、D,进而可得答案.解答:由图象可知当x=0,x=3,x=6时,f(x)=0,
此时函数
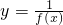 无意义,而选项A、C、D均违背定义域,
无意义,而选项A、C、D均违背定义域,故排除A、C、D,
故选B.
点评:本题考查函数单调性的判断,涉及函数的定义的应用,属基础题.

练习册系列答案
相关题目
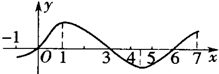 设定义在[-1,7]上的函数y=f(x)的图象如图所示.已知(a,b)是
设定义在[-1,7]上的函数y=f(x)的图象如图所示.已知(a,b)是 (2013•揭阳二模)设定义在[-1,7]上的函数y=f(x)的图象如图示,则关于函数
(2013•揭阳二模)设定义在[-1,7]上的函数y=f(x)的图象如图示,则关于函数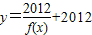 的一个单调递增区间,则b-a的最大值为( )
的一个单调递增区间,则b-a的最大值为( )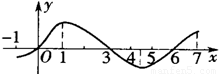
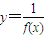 的单调区间表述正确的是( )
的单调区间表述正确的是( )