题目内容
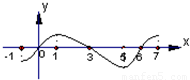
设定义在[-1，7]上的函数y=f（x）的图象如图所示．已知（a，b）是y=| 2012 |
| f(x) |
分析：由y=
+2012可知，函数y=f（x）的单调性与y=
+2012的单调性相反，由y=f（x）的图象可得其递减区间为[1，4]，于是y=
+2012的递增区间为[1，3），（3，4]，从而可得答案．
| 2012 |
| f(x) |
| 2012 |
| f(x) |
| 2012 |
| f(x) |
解答：解：∵函数y=f（x）的单调性与y=
+2012的单调性相反，
∴y=
+2012的单调递增区间就是函数y=f（x）的单调递减区间，
由函数y=f（x）的图象可得其递减区间为[1，4]，当x=3时，f（3）=0，此时y=
+2012无意义，
∴y=
+2012的递增区间为[1，3），（3，4]，
∴b-a的最大值为3-1=2．
故选A．
| 2012 |
| f(x) |
∴y=
| 2012 |
| f(x) |
由函数y=f（x）的图象可得其递减区间为[1，4]，当x=3时，f（3）=0，此时y=
| 2012 |
| f(x) |
∴y=
| 2012 |
| f(x) |
∴b-a的最大值为3-1=2．
故选A．
点评：本题考查函数的图象，难点在于明确函数y=f（x）的单调性与y=
+2012的单调性之间的关系，易错点在于忽视x=3不在函数y=
+2012的定义域内，其单调增区间是断开的，是难题．
| 2012 |
| f(x) |
| 2012 |
| f(x) |
练习册系列答案
备战中考寒假系列答案
相关题目
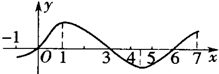
（2013•揭阳二模）设定义在[-1，7]上的函数y=f（x）的图象如图示，则关于函数
设定义在[-1，7]上的函数y=f（x）的图象如图示，则关于函数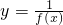
的单调区间表述正确的是
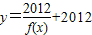的一个单调递增区间，则b-a的最大值为（ ）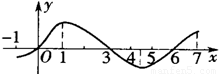
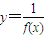的单调区间表述正确的是（ ）