题目内容

已知数列，，

（Ⅰ）当为何值时，数列可以构成公差不为零的等差数列,并求其通项公式；

（Ⅱ）若，令,求数列的前项和。

解:  1）

--------1分

         

    得    -----------------3分

    当 时,       不合题意舍去-----------4分

时,带入可得: ---------------------------5分

   构成以为首项,公差为 -1 的等差数列;------------ ----6分

2）由 可得,,

就有,-------------------------------------------------．8分

即,,又构成以为首项,公比为3 的等比数列;

   ----------10分 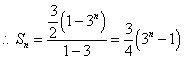  -----------12分

   （若由时,直接得: ;即时,恒成立,

    构成以为首项,公差为1 的等差数列;  www.k@s@5@u.com                            高#考#资#源#网

则． ………该解法不严谨本小题扣2分）

练习册系列答案
相关题目
已知数列an是首项为1的等比数列，Sn是an的前n项和，且S6=9S3，则数列an的通项公式是（　　）
A、2n-1B、21-nC、31-nD、3n-1
已知数列an的前n项和为Sn，a1=2，nan+1=Sn+n（n+1），
（1）求数列an的通项公式；
（2）设bn=
Sn2n
，如果对一切正整数n都有bn≤t，求t的最小值．
已知数列an满足a1=1，an+1=an+n（n∈N*），数列bn满足b1=1，（n+2）bn+1=nbn（n∈N*），数列cn满足c1=1，
c1
1
+
c2
22
+…+
cn
n2
=
cn+1
n+1
（n∈N*）
（1）求数列{an}、{bn}的通项公式；
（2）求数列cn的通项公式；
（3）是否存在正整数k使得k(an+
7
2
)-
3
bn+1
＞cn+6n+15对一切n∈N*恒成立，若存在求k的最小值；若不存在请说明理由．
设数列{an}的前n项和为Sn，Tn=
S1+S2+…+Sn
n
，称Tn为数列a1，a2，…an的“理想数”，已知数列a1，a2，…a500的“理想数”为2004，那么数列2，a1，a2，…a500的“理想数”为（　　）
已知数列
2
、
6
、
10
、
14
、3
2
…那么7
2
是这个数列的第几项（　　）
A、23B、24C、19D、25

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网