题目内容
设 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 N,都有
N,都有
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比q与m函数关系为
的公比q与m函数关系为 ,数列
,数列 满足
满足
 ,
, N,求数列
N,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前 项和
项和 ,使
,使
 恒成立时,求
恒成立时,求 的最小值。
的最小值。
解:(1)证明:当 时,
时, ,解得
,解得 .
.
当 时,
时, . 即
. 即 .
.
∵ 为常数,且
为常数,且 ,∴
,∴
 .∴数列
.∴数列 是首项为1,公比为
是首项为1,公比为 的等比数列.(2)解:由(1)得,
的等比数列.(2)解:由(1)得,
 ,
, .∵
.∵
∴ ,即
,即
 .
.
∴ 是首项为
是首项为 ,公差为1的等差数列.
,公差为1的等差数列.
∴ ,即
,即 (
( ).(3)解:由(2)知
).(3)解:由(2)知 ,则
,则 .所以
.所以 ,
,
即
 , ①
, ① , ②
, ②
②-①得 ,
,
故 .
.

 恒成立,由单调性知当n=1时,右边最大,所以
恒成立,由单调性知当n=1时,右边最大,所以 ,
,

练习册系列答案
相关题目
 的上下顶点分别为
的上下顶点分别为 ,点
,点 在
在 上且直线
上且直线 斜率的取值范围是
斜率的取值范围是 ,那么直线
,那么直线 斜率的取值范围是( )
斜率的取值范围是( ) B.
B. C.
C. D.
D.
 ,x∈
,x∈ ∪
∪ 的图象可能是下列图象中的( )
的图象可能是下列图象中的( )
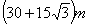 B.
B. 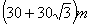 C.
C.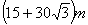 D.
D. 
 .
. ,讨论x的解.
,讨论x的解. ,则
,则 ( )
( ) B.
B.  C .
C .  D.
D. 
 上的点到直线
上的点到直线 的最短距离为
的最短距离为 B.
B. C.
C. D.
D.
 有有理根,那么
有有理根,那么 中至少有一个是偶数。”则假设的内容是 ( )
中至少有一个是偶数。”则假设的内容是 ( )