题目内容
用反证法证明:关于x的方程x2+4ax-4a+3=0、x2+(a-1)x+a2=0、x2+2ax-2a=0,当a≤-
或a≥-1时,至少有一个方程有实数根.
| 3 |
| 2 |
设三个方程都没有实根,
则有判别式都小于零得:
?-
<a<-1,
与a≤-
或a≥-1矛盾,
故原命题成立;
则有判别式都小于零得:
|
| 3 |
| 2 |
与a≤-
| 3 |
| 2 |
故原命题成立;

练习册系列答案
相关题目
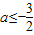 或a≥-1时,至少有一个方程有实数根.
或a≥-1时,至少有一个方程有实数根.