题目内容
已知矩阵
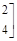 .
.
(1) 求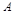 的逆矩阵
的逆矩阵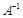 ;
;
(2)求矩阵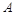 的特征值
的特征值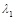 、
、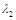 和对应的特征向量
和对应的特征向量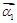 、
、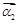 .
.

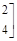 .
.(1) 求
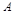 的逆矩阵
的逆矩阵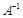 ;
;(2)求矩阵
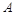 的特征值
的特征值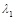 、
、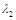 和对应的特征向量
和对应的特征向量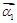 、
、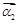 .
.(1) ;(2)当
;(2)当 时,得
时,得 ,当
,当 时,得
时,得 .
.
 ;(2)当
;(2)当 时,得
时,得 ,当
,当 时,得
时,得 .
. 试题分析:(1)求
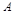 的逆矩阵,首先求出相应的行列式的值,再根据逆矩阵的公式即可写出矩阵A的逆矩阵
的逆矩阵,首先求出相应的行列式的值,再根据逆矩阵的公式即可写出矩阵A的逆矩阵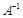 .
.(2)由矩阵
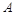 的特征值的共式,
的特征值的共式,
 ,
, 即可求得
即可求得 的值.再由特征值与特征向量的关系即可求出相应的特征向量.
的值.再由特征值与特征向量的关系即可求出相应的特征向量.试题解析:(1)

 ,∴
,∴ .
.(2)矩阵
 的特征多项式为
的特征多项式为

 ,
, 令
 ,得
,得 ,
,当
 时,得
时,得 ,当
,当 时,得
时,得 .
. 
练习册系列答案
相关题目
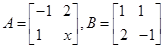 ,向量
,向量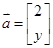 ,
,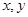 是实数,若
是实数,若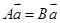 ,求
,求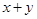 的值.
的值. ,若矩阵
,若矩阵 所对应的变换把直线
所对应的变换把直线 :
: 变换为自身,求
变换为自身,求 .
. ;(2)M=
;(2)M= .
. 当
当 时,函数
时,函数 的最小值为-4,则t的取值范围是
的最小值为-4,则t的取值范围是  +
+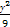 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程. ,矩阵M对应的变换将点(2,1)变换成点(4,-1),求矩阵M将圆x2+y2=1变换后的曲线方程.
,矩阵M对应的变换将点(2,1)变换成点(4,-1),求矩阵M将圆x2+y2=1变换后的曲线方程. 之下的对应点的坐标为(-2,-4),求m、k的值.
之下的对应点的坐标为(-2,-4),求m、k的值.