题目内容
11．记[x]为不超过x的最大整数，若集合S={（x，y）||[x+y]|+|[x-y]|≤1}，则集合S所表示的平面区域的面积为（ ）| A． | $\frac{5}{2}$ | B． | 3 | C． | $\frac{9}{2}$ | D． | 4 |
分析 化简$\left\{\begin{array}{l}{[x+y]=-1}\\{[x-y]=0}\end{array}\right.$或$\left\{\begin{array}{l}{[x+y]=0}\\{-1≤[x-y]≤1}\end{array}\right.$或$\left\{\begin{array}{l}{[x+y]=1}\\{[x-y]=0}\end{array}\right.$，由题意作平面区域，从而求面积．
解答 解：∵|[x+y]|+|[x-y]|≤1，
∴$\left\{\begin{array}{l}{[x+y]=-1}\\{[x-y]=0}\end{array}\right.$或$\left\{\begin{array}{l}{[x+y]=0}\\{-1≤[x-y]≤1}\end{array}\right.$或$\left\{\begin{array}{l}{[x+y]=1}\\{[x-y]=0}\end{array}\right.$，
由题意作平面区域如下，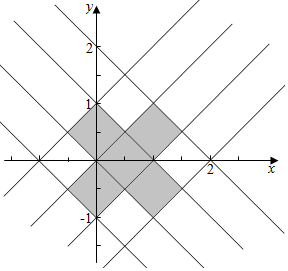
结合图象可知，
面积为5×$\frac{1}{2}$×1×1=$\frac{5}{2}$，
故选A．
点评 本题考查了线性规划的变形应用及数形结合的思想应用，同时考查了分类讨论的思想应用．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
2．已知函数$f（x）=\left\{\begin{array}{l}{2^{x-1}}-2，x≤1\\-{log_2}（x+1），x＞1\end{array}\right.$，且f（a）=-2，则f（a-5）=（ ）
| A． | $-\frac{7}{4}$ | B． | 6 | C． | -10 | D． | $-\frac{15}{8}$ |
如图所示的是某池塘中的浮萍蔓延的面积（m2）与时间t（月）的关系：f（t）=at，有以下叙述：