题目内容
13.若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)-log4|x|的零点个数是( )| A. | 3个 | B. | 2个 | C. | 多于4个 | D. | 4个 |
分析 在同一个坐标系中画出函数y=f(x)的图象与函数y=log4|x|的图象,这两个函数图象的交点个数即为所求.
解答 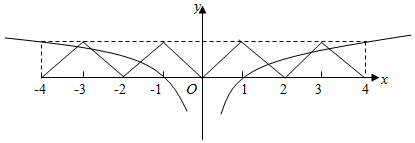 解:∵偶函数f(x)满足f(x+2)=f(x),故函数的周期为2.
解:∵偶函数f(x)满足f(x+2)=f(x),故函数的周期为2.
当x∈[0,1]时,f(x)=x,故当x∈[-1,0]时,f(x)=-x.
函数y=f(x)-log4|x|的零点的个数等于函数y=f(x)的图象与函数y=log4|x|的图象的交点个数.
在同一个坐标系中画出函数y=f(x)的图象与函数y=log4|x|的图象,如图所示:
显然函数y=f(x)的图象与函数y=log4|x|的图象有6个交点,
故选:C
点评 本题考查了根的存在性及根的个数判断,以及函数与方程的思想,根据函数零点和方程的关系进行转化是解决本题的关键.属于中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
1.函数y=x-2,y=2x2,y=(x+1)2,y=3x中,幂函数的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
18.函数y=$\frac{x}{x+a}$在(-2,+∞)上为增函数,则a的取值范围是( )
| A. | a<2 | B. | a≥2 | C. | a≤2 | D. | a>2 |