题目内容
已知函数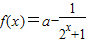 .
.(1)求证:不论a为何实数f(x)总是为增函数;
(2)确定a的值,使f(x)为奇函数;
(3)当f(x)为奇函数时,求f(x)的值域.
【答案】分析:(1)先设x1<x2,欲证明不论a为何实数f(x)总是为增函数,只须证明:f(x1)-f(x2)<0,即可;
(2)根据f(x)为奇函数,利用定义得出f(-x)=-f(x),从而求得a值即可;
(3)由(2)知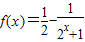 (4),利用指数函数2x的性质结合不等式的性质即可求得f(x)的值域.
(4),利用指数函数2x的性质结合不等式的性质即可求得f(x)的值域.
解答:解:(1)∵f(x)的定义域为R,设x1<x2,
则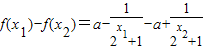 =
=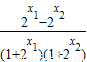 ,
,
∵x1<x2,∴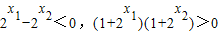 ,∴f(x1)-f(x2)<0,
,∴f(x1)-f(x2)<0,
即f(x1)<f(x2),所以不论a为何实数f(x)总为增函数.
(2)∵f(x)为奇函数,∴f(-x)=-f(x),即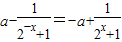 ,
,
解得: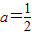 .∴
.∴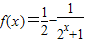 .
.
(3)由(2)知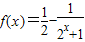 (4),∵2x+1>1(5),∴
(4),∵2x+1>1(5),∴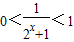 (6),∴
(6),∴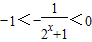 ,∴
,∴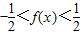
所以f(x)的值域为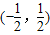 .
.
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力与化归与转化思想.属于基础题.
(2)根据f(x)为奇函数,利用定义得出f(-x)=-f(x),从而求得a值即可;
(3)由(2)知
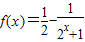 (4),利用指数函数2x的性质结合不等式的性质即可求得f(x)的值域.
(4),利用指数函数2x的性质结合不等式的性质即可求得f(x)的值域.解答:解:(1)∵f(x)的定义域为R,设x1<x2,
则
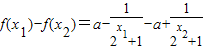 =
=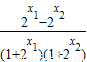 ,
,∵x1<x2,∴
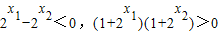 ,∴f(x1)-f(x2)<0,
,∴f(x1)-f(x2)<0,即f(x1)<f(x2),所以不论a为何实数f(x)总为增函数.
(2)∵f(x)为奇函数,∴f(-x)=-f(x),即
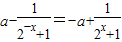 ,
,解得:
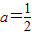 .∴
.∴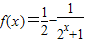 .
.(3)由(2)知
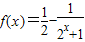 (4),∵2x+1>1(5),∴
(4),∵2x+1>1(5),∴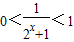 (6),∴
(6),∴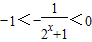 ,∴
,∴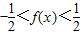
所以f(x)的值域为
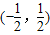 .
.点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力与化归与转化思想.属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目





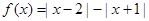 .
. ;
;
 .
. ;
; .
. .
. 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
) 时,若关于
时,若关于 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围. .
. 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
) 时,若关于
时,若关于 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.