题目内容
已知b为二项式（9+x）n展开式中各项系数之和，且
=
，则实数a取值范围是
| lim |
| n→∞ |
| b+an |
| 10b+an+1 |
| 1 |
| a |
（-∞，-10）∪[10，+∞）
（-∞，-10）∪[10，+∞）
．分析：依题意，b=10n，再由
=
⇒|a|≥10且a≠-10，解此不等式即可得答案．
| lim |
| n→∞ |
| 10n+an |
| 10n+1+an+1 |
| 1 |
| a |
解答：解：∵b为二项式（9+x）n展开式中各项系数之和，
∴b=（9+1）n=10n，
∴
=
=
，
∴|a|≥10且a≠-10，
∴a＜-10或a≥10．
∴实数a取值范围是a＜-10或a≥10．
故答案为：（-∞，-10）∪[10，+∞）．
∴b=（9+1）n=10n，
∴
| lim |
| n→∞ |
| b+an |
| 10b+an+1 |
| lim |
| n→∞ |
| 10n+an |
| 10n+1+an+1 |
| 1 |
| a |
∴|a|≥10且a≠-10，
∴a＜-10或a≥10．
∴实数a取值范围是a＜-10或a≥10．
故答案为：（-∞，-10）∪[10，+∞）．
点评：本题考查求极限，考查二项式系数的性质，求得b=10n，继而求得|a|≥10且a≠-10是关键，也是难点，忽略a≠-10是易错点，考查缜密思维，细心思维，属于难题．
练习册系列答案
相关题目
，则实数a的取值范围是
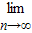
，则实数a取值范围是 ．
，则实数a取值范围是 ．