题目内容

5．设a+b=3，则直线ax+by=1恒过定点（$\frac{1}{3}$，$\frac{1}{3}$）．

分析 根据条件方程a+b=3可化为a•$\frac{1}{3}$+b•$\frac{1}{3}$=1，即可得出直线ax+by=1恒过定点．

解答 解：∵a+b=3，
∴a•$\frac{1}{3}$+b•$\frac{1}{3}$=1，
∴直线ax+by=1恒过定点（$\frac{1}{3}$，$\frac{1}{3}$）．
故答案为：（$\frac{1}{3}$，$\frac{1}{3}$）．

点评 本题考查恒过定点的直线系问题，方程a+b=3化为a•$\frac{1}{3}$+b•$\frac{1}{3}$=1是关键．

练习册系列答案
相关题目
15．已知角φ（|φ|＜$\frac{π}{2}$）的顶点为原点，终边经过点P（1，-1），点A（x1，y1），B（x2，y2）是函数f（x）=2sin（ωx+φ）（ω＞0）图象上任意两点，若|f（x1）-f（x2）|=4时，|x1-x2|的最小值为$\frac{π}{3}$．
（1）求函数f（x）的解析式；
（2）将f（x）的图象向左平移$\frac{π}{3}$个单位，再将f（x）的图象的每个点保持纵坐标不变，横坐标缩短为原来的$\frac{1}{3}$，得到y=g（x）的图象，求y=g（x）在[-$\frac{π}{12}$，$\frac{π}{3}$]上的递增区间．
16．已知6a=8．试用a表示下列各式：
①log68；
②1og62；
③log26．
13．求函数f（x）=x2-2ax-1在区间[0，2]上的最值．
20．$\sqrt{1-2sin\frac{7}{6}π•cos\frac{7}{6}π}$．
10．如果a＜bc，那么（　　）
A．a＜bB．a＜cC．ac2＜bc3D．a-c＜（b-1）c
17．在等比数列{an}中，
（1）已知a1=2，q=3．求S3；
（2）求等比数列1，$\frac{1}{2}$，$\frac{1}{8}$，…的前5项的和．
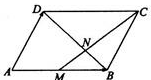14．已知平行四边形ABCD中，$\overrightarrow{AD}$=$\overrightarrow{a}$，$\overrightarrow{AB}$=$\overrightarrow{b}$，M为AB中点，N为BD靠近B的三等分点．
（1）用基底$\overrightarrow{a}$，$\overrightarrow{b}$表示向量$\overrightarrow{MC}$、$\overrightarrow{NC}$；
（2）求证：M，N，C三点共线．
15．求函数f（x）=2${\;}^{{x}^{2}-6x+17}$定义域、值域、单调区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网