题目内容
如图所示，多面体ABCDS中，面
为矩形，SD⊥AD，SD⊥AB，且
，
，M、N分别为AB、CD中点.
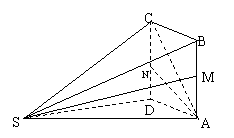
（Ⅰ）求证：SM⊥AN；
（Ⅱ）求二面角A―SC―D的余弦值；
（Ⅲ）若AB=
，求点D到平面ASC的距离.
解：（I）建立如图所示的空间直角坐标系，设AD=1，
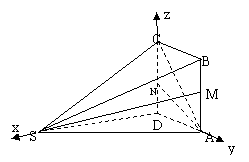
则A(0,1,0),N(0,0,1),S(
,0,0),M(0,1,1),C(0,0,2)
,
∴SM⊥SM
（Ⅱ）设平面SAS的法向量为
，
，
=(0,-1,2)
则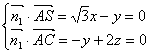
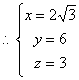
又平面SDC的一个法向量
设二面角A－SC－D的平面角为θ，
则
∴二面角A－SC－D的余弦值为
（Ⅲ）∵
平面ASC法向量为
∴D到平面ASC的距离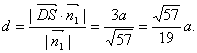
练习册系列答案
相关题目
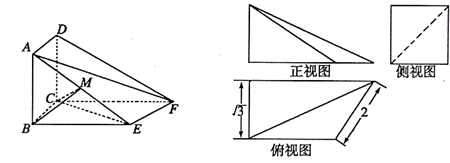
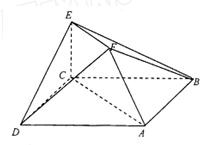在如图所示的多面体中，已知正方形ABCD和直角梯形ACEF所在的平面互相垂直，EC⊥AC，EF∥AC，AB=
在如图所示的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC．BC=2AD=4，EF=3，AE=BE=2，G为BC的中点．
如图所示，多面体EF-ABCD中，ABCD是直角梯形，AB⊥AD，AB∥DC，∠ABC=60°，FC⊥平面ABCD，正△ADE⊥平面ABCD，