题目内容
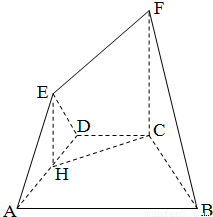
 如图所示,多面体EF-ABCD中,ABCD是直角梯形,AB⊥AD,AB∥DC,∠ABC=60°,FC⊥平面ABCD,正△ADE⊥平面ABCD,FC=2DC=6,AD=2
如图所示,多面体EF-ABCD中,ABCD是直角梯形,AB⊥AD,AB∥DC,∠ABC=60°,FC⊥平面ABCD,正△ADE⊥平面ABCD,FC=2DC=6,AD=2| 3 |
(1)求证:BC⊥平面EFCH;
(2)求二面角H-BF-C的平面角的余弦值.
分析:(1)证明BC⊥平面EFCH,利用线面垂直的判定,只需证明BC⊥CH,BC⊥FC即可;
(2)过C作CG⊥FB,垂足为G,连接HG,证明∠HGC为二面角H-BF-C的平面角,计算CG,HG,即可求得二面角H-BF-C的平面角的余弦值.
(2)过C作CG⊥FB,垂足为G,连接HG,证明∠HGC为二面角H-BF-C的平面角,计算CG,HG,即可求得二面角H-BF-C的平面角的余弦值.
解答:(1)证明:在△DHC中,∠HDC=90°,DC=3,DH=
,∴CH=2
,∴∠DCH=30°
∵AB∥DC,∠ABC=60°,∴∠BCH=90°,∴BC⊥CH
∵H为AD中点,△ADE为正三角形
∴EH⊥AD
∵正△ADE⊥平面ABCD,△ADE∩平面ABCD=AD
∴EH⊥平面ABCD
∵FC⊥平面ABCD
∴EH∥FC
∴EFCH是平面四边形
∵FC⊥平面ABCD,CB?平面ABCD
∴BC⊥FC
∵FC∩CH=C
∴BC⊥平面EFCH;
(2)过C作CG⊥FB,垂足为G,连接HG,
∵FC⊥平面ABCD,HC?平面ABCD
∴HC⊥FC
∵HC⊥BC,FC∩BC=C
∴HC⊥平面BCF
∵CG⊥FB,∴HG⊥FB
∴∠HGC为二面角H-BF-C的平面角
在直角△BCF中,CF=6,BC=4,则BF=2
,∴CG=
=
在△HCF中,HC=2
,CG=
,∴HG=
∴cos∠HGC=
=
∴二面角H-BF-C的平面角的余弦值为
| 3 |
| 3 |
∵AB∥DC,∠ABC=60°,∴∠BCH=90°,∴BC⊥CH
∵H为AD中点,△ADE为正三角形
∴EH⊥AD
∵正△ADE⊥平面ABCD,△ADE∩平面ABCD=AD
∴EH⊥平面ABCD
∵FC⊥平面ABCD
∴EH∥FC
∴EFCH是平面四边形
∵FC⊥平面ABCD,CB?平面ABCD
∴BC⊥FC
∵FC∩CH=C
∴BC⊥平面EFCH;
(2)过C作CG⊥FB,垂足为G,连接HG,

∵FC⊥平面ABCD,HC?平面ABCD
∴HC⊥FC
∵HC⊥BC,FC∩BC=C
∴HC⊥平面BCF
∵CG⊥FB,∴HG⊥FB
∴∠HGC为二面角H-BF-C的平面角
在直角△BCF中,CF=6,BC=4,则BF=2
| 13 |
| CF×BC |
| BF |
12
| ||
| 13 |
在△HCF中,HC=2
| 3 |
12
| ||
| 13 |
| 5 |
| 13 |
| 156 |
∴cos∠HGC=
| CG |
| HG |
| ||
| 5 |
∴二面角H-BF-C的平面角的余弦值为
| ||
| 5 |
点评:本题考查线面垂直,考查面面角,解题的关键是掌握线面垂直的判定,正确作出面面角,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
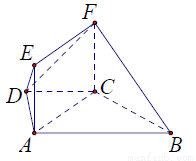
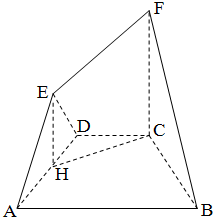 如图所示,多面体EF-ABCD中,ABCD是直角梯形,AB⊥AD,AB∥DC,∠ABC=60°,FC⊥平面ABCD,正△ADE⊥平面ABCD,
如图所示,多面体EF-ABCD中,ABCD是直角梯形,AB⊥AD,AB∥DC,∠ABC=60°,FC⊥平面ABCD,正△ADE⊥平面ABCD,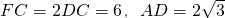 ,H为AD中点.
,H为AD中点. 。
。
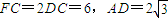 ,H为AD中点.
,H为AD中点.