题目内容
14.已知直线l:2x+(m+1)y+2m=0(m∈R)在x轴上的截距等于它在y轴上的截距的2倍,求直线l的方程.分析 分别令x=0,y=0,求出截距,由题意得到-m=-2×$\frac{2m}{m+1}$,解得m的值,即可求出直线方程.
解答 解:∵2x+(m+1)y+2m=0(m∈R),
令x=0,得y=-$\frac{2m}{m+1}$,令y=0,得x=-m,
∵直线l:2x+(m+1)y+2m=0(m∈R)在x轴上的截距等于它在y轴上的截距的2倍,
∴-m=-2×$\frac{2m}{m+1}$,
解得m=3或m=0,
当m=0时,直线为2x+y=0,
当m=3时,直线为x+2y+3=0.
点评 本题考查了求直线方程的应用问题,也考查了分类讨论方法的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.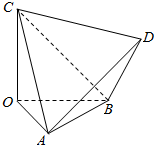 在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
 在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )
在如图所示的几何体中,三棱锥D-ABC的各条棱长均为2,OA,OB,OC两两垂直,则下列说法正确的是( )| A. | OA,OB,OC的长度可以不相等 | B. | 直线OB∥平面ACD | ||
| C. | 直线OD与BC所成的角是45° | D. | 直线AD与OB所成的角是45° |
5.某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A. | 72cm3 | B. | 90cm3 | C. | 108cm3 | D. | 138cm3 |
9.已知直线l的方向向量为$\overrightarrow{a}$=(1,0,2),平面α的法向量$\overrightarrow{n}$=(-1,0,-2),则( )
| A. | l?α | B. | l⊥α | C. | l∥α | D. | l与α斜交 |
19.已知函数f(x)=$\left\{\begin{array}{l}{|{2}^{x}-1|,x<2}\\{\frac{3}{x-1},x≥2}\end{array}\right.$,若函数g(x)=f(x)-loga8有两个不同的零点,则实数a的取值范围是( )
| A. | [$\frac{1}{8}$,1)∪(1,2] | B. | (2,8) | C. | (2,+∞) | D. | (2,8] |