题目内容
给出四个命题
①若cosα=cosβ，则α-β=2kπ，k∈Z．
②函数y=2cos(2x+
)的图象关于点(
，0)对称．
③函数y=sin|x|是周期函数．
④函数y=cos（sinx）（x∈R）是偶函数．
其中正确的是
①若cosα=cosβ，则α-β=2kπ，k∈Z．
②函数y=2cos(2x+
| π |
| 3 |
| π |
| 12 |
③函数y=sin|x|是周期函数．
④函数y=cos（sinx）（x∈R）是偶函数．
其中正确的是
②④
②④
．分析：利用三角函数的图象和性质，分别进行判断．
解答：解：①若cosα=cosβ，则α=β+2kπ或者α=-β+2kπ，所以α-β=2kπ，k∈Z或α+β=2kπ，k∈Z，所以①错误．
②当x=
时，y=f(
)=2cos(2×
+
)=2cos
=0，所以函数y=2cos(2x+
)的图象关于点(
，0)对称．所以②正确．
③根据函数y=sin|x|的图象特征可得，函数y=sin|x|不是周期函数，故③不正确．
④因为f（-x）=cos（sin（-x））=cos（-sinx）=cos（sinx）=f（x），所以函数y=cos（sinx）（x∈R）是偶函数，所以④正确．
故答案为：②④．
②当x=
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 12 |
③根据函数y=sin|x|的图象特征可得，函数y=sin|x|不是周期函数，故③不正确．
④因为f（-x）=cos（sin（-x））=cos（-sinx）=cos（sinx）=f（x），所以函数y=cos（sinx）（x∈R）是偶函数，所以④正确．
故答案为：②④．
点评：本题主要考查三角函数的图象和性质，综合性较强．
练习册系列答案
相关题目
.
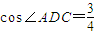，则其中正确命题的序号为 ．