题目内容
已知正方形ABCD,AC,BD交于点O,若将正方形沿BD折成60°的二面角,并给出四个结论:(1)AC⊥BD;
(2)AD⊥CO;
(3)△AOC为正三角形;
(4)
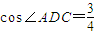 ,则其中正确命题的序号为 .
,则其中正确命题的序号为 .
【答案】分析:令正方形ABCD的边长为1,画出对折后的图形,对四个答案逐一进行分析,不难得到答案.
解答: 解:如图,
解:如图,
(1)∵BD⊥AO,BD⊥CO∴BD⊥面OAC∴AC⊥BD.故(1)正确
(2)∵CO与面ABD不垂直,CO⊥BD∴CO与AD不垂直,故(2)错误
(3)∵BD⊥AO,BD⊥CO,面ABD与面BCD成60°的二面角
∴∠AOC=60°,又∵OA=OC∴)△AOC为正三角形,故(3)正确
(4)∵AD=CD=1,AC=OC= ,由余弦定理得:cos∠ADC=
,由余弦定理得:cos∠ADC= ,故(4)正确
,故(4)正确
故答案为:(1)、(3)、(4)
点评:在判断空间线面的关系,常常把他们放在空间几何体中来直观的分析,在判断线与面的平行与垂直关系时,正方体是最常用的空间模型,大家一定要熟练掌握这种方法.
解答:
 解:如图,
解:如图,(1)∵BD⊥AO,BD⊥CO∴BD⊥面OAC∴AC⊥BD.故(1)正确
(2)∵CO与面ABD不垂直,CO⊥BD∴CO与AD不垂直,故(2)错误
(3)∵BD⊥AO,BD⊥CO,面ABD与面BCD成60°的二面角
∴∠AOC=60°,又∵OA=OC∴)△AOC为正三角形,故(3)正确
(4)∵AD=CD=1,AC=OC=
 ,由余弦定理得:cos∠ADC=
,由余弦定理得:cos∠ADC= ,故(4)正确
,故(4)正确故答案为:(1)、(3)、(4)
点评:在判断空间线面的关系,常常把他们放在空间几何体中来直观的分析,在判断线与面的平行与垂直关系时,正方体是最常用的空间模型,大家一定要熟练掌握这种方法.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
已知正方形ABCD边长为1,则|
+
+
|=( )
| AB |
| BC |
| AC |
| A、0 | ||
| B、2 | ||
C、
| ||
D、2
|
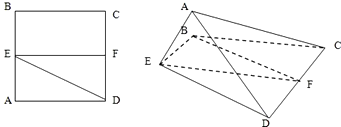 已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π). (2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
(2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,