题目内容
在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C：ρsin2θ=2acosθ（a＞0），过点P（-2，-4）的直线l的参数方程为
（t为参数），l与C分别交于M，N．
|
考点：简单曲线的极坐标方程,参数方程化成普通方程
专题：坐标系和参数方程
分析：（1）利用极坐标与普通方程的关系式，可得C为抛物线方程，消去参数t，可得直线l的方程；
（2）由|PM|=|t1|，|MN|=|t1-t2|，|PN|=|t2|成等比数列，可转化为关于a的等量关系求解．
（2）由|PM|=|t1|，|MN|=|t1-t2|，|PN|=|t2|成等比数列，可转化为关于a的等量关系求解．
解答：
解：（Ⅰ）曲线C：ρsin2θ=2acosθ，可得ρ2sin2θ=2aρcosθ，它的直角坐标方程为y2=2ax（a＞0）；
，消去t，可得x-y-2=0，
直线l的普通方程为x-y-2=0． 4分
（Ⅱ）将直线l的参数方程与C的直角坐标方程联立，得
t2-2（4+a）
t+8（4+a）=0 （*）
△=8a（4+a）＞0．
设点M，N分别对应参数t1，t2，恰为上述方程的根．
则|PM|=|t1|，|PN|=|t2|，|MN|=|t1-t2|．
由题设得（t1-t2）2=|t1t2|，即（t1+t2）2-4t1t2=|t1t2|．
由（*）得t1+t2=2（4+a）
，t1t2=8（4+a）＞0，则有
（4+a）2-5（4+a）=0，得a=1，或a=-4．
因为a＞0，所以a=1． 10分
|
直线l的普通方程为x-y-2=0． 4分
（Ⅱ）将直线l的参数方程与C的直角坐标方程联立，得
t2-2（4+a）
| 2 |
△=8a（4+a）＞0．
设点M，N分别对应参数t1，t2，恰为上述方程的根．
则|PM|=|t1|，|PN|=|t2|，|MN|=|t1-t2|．
由题设得（t1-t2）2=|t1t2|，即（t1+t2）2-4t1t2=|t1t2|．
由（*）得t1+t2=2（4+a）
| 2 |
（4+a）2-5（4+a）=0，得a=1，或a=-4．
因为a＞0，所以a=1． 10分
点评：本题考查参数方程与极坐标的应用，基本知识的考查．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
已知动点M与F（1，0）的距离比它到直线l：x+3=0的距离小2，设M的轨迹为G，正项数列{an}满足a1=2，且（an，
）在曲线G上，则数列{an}的通项公式为（ ）
| 2an+1 |
| A、an=2n |
| B、an=2n-1 |
| C、an=2n+1 |
| D、an=2-1 |
两条不重合的直线m，n以及两个平面α，β，给出下列命题：
①若m∥α，n∥α，则m∥n；
②若m∥α，n⊥α，则m⊥n；
③若m∥n，n∥α，则m∥α；
④若m⊥α，m∥β，则α⊥β；
其中真命题的个数为（ ）
①若m∥α，n∥α，则m∥n；
②若m∥α，n⊥α，则m⊥n；
③若m∥n，n∥α，则m∥α；
④若m⊥α，m∥β，则α⊥β；
其中真命题的个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
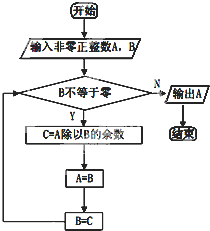在如图的算法中，如果输入A=138，B=22，则输出的结果是（ ）| A、2 | B、4 | C、128 | D、0 |