题目内容
已知函数f(x)=loga(ax- )(a>0,a≠1为常数).
)(a>0,a≠1为常数).
(1)求函数f(x)的定义域;
(2)若a=2,x∈[1,9],求函数f(x)的值域.
解:(1)ax- >0⇒
>0⇒ (a
(a -1)>0,∵
-1)>0,∵ >0,
>0,
∴a -1>0,∵a>0,∴
-1>0,∵a>0,∴ >
> .
.
∴x> ,所以定义域为(
,所以定义域为( ,+∞).----------------------------------6
,+∞).----------------------------------6
(2)a=2时,f(x)=log2(2x- ),令2x-
),令2x- =t则
=t则
t=2x- =2(
=2( -
-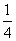 )2
)2  ---------------------------------8
---------------------------------8
因为x∈[1,9],所以t∈[1,15],----------------------------------10
所以log21≤log2(2x- )≤log215,即0≤f(x)≤log215
)≤log215,即0≤f(x)≤log215
所以函数f(x)的值域为[0,log215].--------------------------12

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
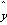 =
= -
-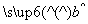
 =42-9.4×3.5=9.1,所以线性回归方程是
=42-9.4×3.5=9.1,所以线性回归方程是 =65.5.
=65.5.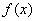 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( ) B.
B.
 D.
D.
 的图象不过原点,则实数m的值是________.
的图象不过原点,则实数m的值是________. ,
, ,则
,则 ( )
( ) |0<
|0< } B.{
} B.{ ,且函数f(x)=
,且函数f(x)= 的最小值为b,若函数g(x)=
的最小值为b,若函数g(x)= ,则不等式g(x)≤1的解集为 ( )
,则不等式g(x)≤1的解集为 ( ) B.
B. C.
C. D.
D.
 B.频率为
B.频率为 的概率是________.
的概率是________.