题目内容
复数z=1-cosθ+isinθ(2π<θ<3π)的模为( )A.2cos

B.-2cos

C.2sin

D.-2sin

【答案】分析:法一:把复数的代数形式利用二倍角公式及诱导公式化为复数的三角形式,通过三角形式求复数的模.
法二:利用复数的模的定义直接列出式子,并利用三角公式化简.
解答:解:方法一:复数z=1-cosθ+isinθ=1-(1-2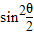 )+i•2sin
)+i•2sin cos
cos =2sin
=2sin [cos(
[cos(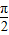 -
- )+isin(
)+isin( -
- )]
)]
=-2sin [cos(π+
[cos(π+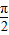 -θ)+isin(π+
-θ)+isin(π+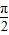 -θ)].
-θ)].
∵2π<θ<3π,∴π< <
<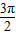 ,-π<
,-π< -
- <-
<-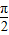 ,∴0<π+
,∴0<π+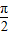 -θ<
-θ<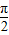 ,
,
∴sin <0,-2sin
<0,-2sin >0,
>0,
∴z=1-cosθ+isinθ(2π<θ<3π)的模为-sin ,
,
故选 D.
方法二:|z|=|1-cosθ+isinθ|=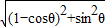 =
=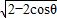 =
=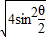
=2|sin |,
|,
∵2π<θ<3π,∴π< <
<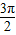 ,∴sin
,∴sin <0,-2sin
<0,-2sin >0,
>0,
∴|z|=2|sin |=-2sin
|=-2sin .
.
故选 D.
点评:本题考查复数的模的定义,利用三角公式及角的范围、三角函数的符号来求复数的模.
法二:利用复数的模的定义直接列出式子,并利用三角公式化简.
解答:解:方法一:复数z=1-cosθ+isinθ=1-(1-2
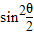 )+i•2sin
)+i•2sin cos
cos =2sin
=2sin [cos(
[cos(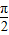 -
- )+isin(
)+isin( -
- )]
)]=-2sin
 [cos(π+
[cos(π+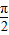 -θ)+isin(π+
-θ)+isin(π+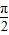 -θ)].
-θ)].∵2π<θ<3π,∴π<
 <
<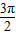 ,-π<
,-π< -
- <-
<-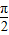 ,∴0<π+
,∴0<π+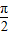 -θ<
-θ<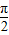 ,
,∴sin
 <0,-2sin
<0,-2sin >0,
>0,∴z=1-cosθ+isinθ(2π<θ<3π)的模为-sin
 ,
,故选 D.
方法二:|z|=|1-cosθ+isinθ|=
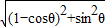 =
=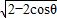 =
=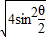
=2|sin
 |,
|,∵2π<θ<3π,∴π<
 <
<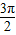 ,∴sin
,∴sin <0,-2sin
<0,-2sin >0,
>0,∴|z|=2|sin
 |=-2sin
|=-2sin .
.故选 D.
点评:本题考查复数的模的定义,利用三角公式及角的范围、三角函数的符号来求复数的模.

练习册系列答案
相关题目
复数z=1-cosθ+isinθ(2π<θ<3π)的模为( )
A、2cos
| ||
B、-2cos
| ||
C、2sin
| ||
D、-2sin
|