题目内容
已知cos(α-
)=-
,sin(
-β)=
,且α∈(
,π),β∈(0,
).求:
(1)cos
;
(2)tan(α+β).
| β |
| 2 |
2
| ||
| 7 |
| α |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
(1)cos
| α+β |
| 2 |
(2)tan(α+β).
考点:两角和与差的正切函数
专题:三角函数的求值
分析:(1)利用cos
=cos[(α-
)-(
-β)],求出相关的三角函数值即可求解;
(2)求出相关角的范围,利用tan(α+β)=
,求解即可.
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
(2)求出相关角的范围,利用tan(α+β)=
2tan
| ||
1-tan2
|
解答:
解:(1)cos(α-
)=-
,且α∈(
,π),β∈(0,
).α-
∈(
,π),
∴sin(α-
)=
=
.
sin(
-β)=
,且α∈(
,π),β∈(0,
).
-β∈(-
,
).
cos(
-β)=
=
.
cos
=cos[(α-
)-(
-β)]=-
×
+
×
=-
.
(2)α∈(
,π),β∈(0,
).α+β∈(
,
),
∈(
,
),
∵cos
=-
.
∴
∈(
,
),
sin
=
=
,
tan
=-
.
tan(α+β)=
=
=
.
| β |
| 2 |
2
| ||
| 7 |
| π |
| 2 |
| π |
| 2 |
| β |
| 2 |
| π |
| 4 |
∴sin(α-
| β |
| 2 |
1-cos2(α-
|
| ||
| 7 |
sin(
| α |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| α |
| 2 |
| π |
| 4 |
| π |
| 2 |
cos(
| α |
| 2 |
1-sin2(
|
| ||
| 2 |
cos
| α+β |
| 2 |
| β |
| 2 |
| α |
| 2 |
2
| ||
| 7 |
| ||
| 2 |
| ||
| 7 |
| 1 |
| 2 |
| ||
| 14 |
(2)α∈(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
| α+β |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
∵cos
| α+β |
| 2 |
| ||
| 14 |
∴
| α+β |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
sin
| α+β |
| 2 |
1-cos2
|
| ||
| 14 |
tan
| α+β |
| 2 |
| ||
| 3 |
tan(α+β)=
2tan
| ||
1-tan2
|
2×(-
| ||||
1-(-
|
| ||
| 11 |
点评:本题考查二倍角公式的应用,同角三角函数的基本关系式的应用,注意角的范围,考查计算能力.

练习册系列答案
相关题目
已知A(-2,0),B(0,2),实数k是常数,M,N是圆x2+y2+kx=0上两个不同点,且M,N关于直线x-y-1=0对称,若P是圆x2+y2+kx=0上的动点,则△PAB面积的最大值是( )
A、3-
| ||
| B、4 | ||
C、3+
| ||
| D、6 |
如图所示是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入( )
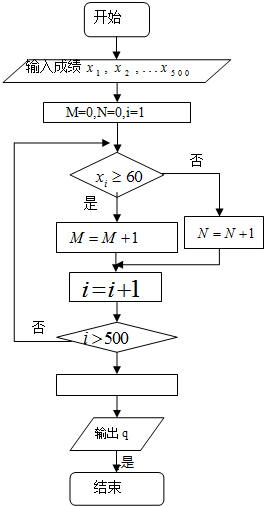

A、q=
| ||
B、q=
| ||
C、q=
| ||
D、q=
|
设函数f(x)在R上可导,且f(x-1)=x2-2x,则f′(3)=( )
| A、0 | B、4 | C、6 | D、8 |