题目内容
已知函数 的反函数为f-1(x),数列{an}满足:a1=1,an+1=f-1(an)(n∈N*).
的反函数为f-1(x),数列{an}满足:a1=1,an+1=f-1(an)(n∈N*).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足:
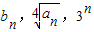 成等比数列,数列{bn}的前n项和为Sn,求Sn.
成等比数列,数列{bn}的前n项和为Sn,求Sn.
【答案】分析:(1)先求原函数的反函数,即从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式,再利用等差数列求数列 的通项,最后求出数列{an}的通项.
的通项,最后求出数列{an}的通项.
(2)据 成等比数列求得数列{bn}的通项,再利用错位相乘法求其前n项和即可.
成等比数列求得数列{bn}的通项,再利用错位相乘法求其前n项和即可.
解答:解:(Ⅰ)∵ =
= (x≥4),
(x≥4),
∴f-1(x)= (x≥0),
(x≥0),
∴an+1=f-1(an)= ,
,
即 (n∈N*).
(n∈N*).
∴数列 是以
是以 为首项,公差为2的等差数列.
为首项,公差为2的等差数列.
∴ ,即an=(2n-1)2(n∈N*).
,即an=(2n-1)2(n∈N*).
(Ⅱ)∵ 成等比数列,∴
成等比数列,∴
从而 (n∈N*).
(n∈N*).
∴Sn=b1+b2++bn=
则
两式相减得 =
=
∴ .
.
点评:本题考查反函数的求法,以及等差数列等比数列的通项公式和性质,还有错位相头减法求数列的前n项和.属于中档题.
 的通项,最后求出数列{an}的通项.
的通项,最后求出数列{an}的通项.(2)据
 成等比数列求得数列{bn}的通项,再利用错位相乘法求其前n项和即可.
成等比数列求得数列{bn}的通项,再利用错位相乘法求其前n项和即可.解答:解:(Ⅰ)∵
 =
= (x≥4),
(x≥4),∴f-1(x)=
 (x≥0),
(x≥0),∴an+1=f-1(an)=
 ,
,即
 (n∈N*).
(n∈N*).∴数列
 是以
是以 为首项,公差为2的等差数列.
为首项,公差为2的等差数列.∴
 ,即an=(2n-1)2(n∈N*).
,即an=(2n-1)2(n∈N*).(Ⅱ)∵
 成等比数列,∴
成等比数列,∴
从而
 (n∈N*).
(n∈N*).∴Sn=b1+b2++bn=

则

两式相减得
 =
=
∴
 .
.点评:本题考查反函数的求法,以及等差数列等比数列的通项公式和性质,还有错位相头减法求数列的前n项和.属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 的反函数为f-1(x),数列{an}满足:a1=1,an+1=f-1(an)(n∈N*).
的反函数为f-1(x),数列{an}满足:a1=1,an+1=f-1(an)(n∈N*). 成等比数列,数列{bn}的前n项和为Sn,求Sn.
成等比数列,数列{bn}的前n项和为Sn,求Sn.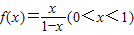 的反函数为f-1(x).设数列{an}满足a1=1,an+1=f-1(an)(n∈N*).
的反函数为f-1(x).设数列{an}满足a1=1,an+1=f-1(an)(n∈N*).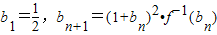 ,求证:对一切正整数n≥1都有
,求证:对一切正整数n≥1都有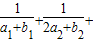 …
…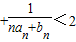 .
. 的反函数为f-1(x),若f-1(x)>0,则x的取值范围为 .
的反函数为f-1(x),若f-1(x)>0,则x的取值范围为 . 的反函数为f-1(x),则f-1(4)=( )
的反函数为f-1(x),则f-1(4)=( )