题目内容
【题目】已知 ![]() ,
, ![]() ,
, ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(﹣
=(﹣ ![]() ,1).
,1).
(1)若| ![]() |=2 且
|=2 且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,(
,( ![]() +3
+3 ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),求向量
),求向量 ![]() ,
, ![]() 的夹角的余弦值.
的夹角的余弦值.
【答案】
(1)解:设 ![]() =(m,n),
=(m,n),
若| ![]() |=2 且
|=2 且 ![]() ∥
∥ ![]() ,其中
,其中 ![]() =(﹣
=(﹣ ![]() ,1),
,1),
可得m2+n2=4,m=﹣ ![]() n,
n,
解得m=﹣ ![]() ,n=
,n= ![]() 或m=
或m= ![]() ,n=﹣
,n=﹣ ![]() ,
,
则 ![]() =(﹣
=(﹣ ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() )
)
(2)解:若 ![]() =(﹣
=(﹣ ![]() ,1),可得|
,1),可得| ![]() |=
|= ![]() ,
,
又| ![]() |=
|= ![]() ,(
,( ![]() +3
+3 ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),
),
可得( ![]() +3
+3 ![]() )(
)( ![]() ﹣
﹣ ![]() )=
)= ![]() 2﹣3
2﹣3 ![]() 2+2
2+2 ![]()
![]() =0,
=0,
即有3﹣3×2+2 ![]()
![]() =0,
=0,
可得 ![]()
![]() =
= ![]() ,
,
向量 ![]() ,
, ![]() 的夹角的余弦值为
的夹角的余弦值为 ![]() =
= 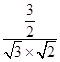 =
= ![]()
【解析】(1)设 ![]() =(m,n),运用向量模的公式和向量共线的坐标表示,解方程即可得到所求;(2)由向量垂直的条件:数量积为0,以及向量的平方即为模的平方,化简整理,可得
=(m,n),运用向量模的公式和向量共线的坐标表示,解方程即可得到所求;(2)由向量垂直的条件:数量积为0,以及向量的平方即为模的平方,化简整理,可得 ![]()
![]() =
= ![]() ,再由向量夹角的余弦公式,计算即可得到所求值.
,再由向量夹角的余弦公式,计算即可得到所求值.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目