题目内容
点M(3,4)到圆x2+y2=1上一点的最大值等于________.
6
分析:M(3,4)与圆心的连线的延长线与该圆的交点之间的距离就是M(3,4)到圆x2+y2=1上一点的最大值.
解答:∵圆x2+y2=1的圆心O(0,0),
∴|MO|= =5,设MO的延长线与圆x2+y2=1相交于P,
=5,设MO的延长线与圆x2+y2=1相交于P,
则|MP|即为点M(3,4)到圆x2+y2=1上一点的最大值,
而|MP|=5+1=6.
故答案为:6.
点评:本题考查点与圆的位置关系,关键在于把握M(3,4)与圆心的连线的延长线与该圆的交点之间的距离就是所求,属于基础题.
分析:M(3,4)与圆心的连线的延长线与该圆的交点之间的距离就是M(3,4)到圆x2+y2=1上一点的最大值.
解答:∵圆x2+y2=1的圆心O(0,0),
∴|MO|=
 =5,设MO的延长线与圆x2+y2=1相交于P,
=5,设MO的延长线与圆x2+y2=1相交于P,则|MP|即为点M(3,4)到圆x2+y2=1上一点的最大值,
而|MP|=5+1=6.
故答案为:6.
点评:本题考查点与圆的位置关系,关键在于把握M(3,4)与圆心的连线的延长线与该圆的交点之间的距离就是所求,属于基础题.

练习册系列答案
相关题目

 已知椭圆
已知椭圆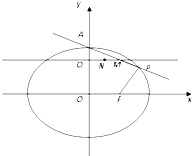 已知椭圆
已知椭圆 的离心率为
的离心率为 ,且过点P(4,
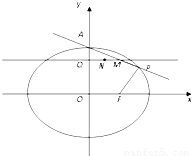
,且过点P(4, ),A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
),A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.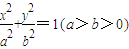 的离心率为
的离心率为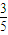 ,且过点P(4,
,且过点P(4,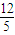 ),A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
),A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.