题目内容
求证:
证法一:欲证原命题成立,即证(![]() -
-![]() )(
)(![]() -3)≤0,
-3)≤0,
即![]() ·
·![]() ≤0,
≤0,
即-![]() ·
·![]() ≤0.
≤0.
上式显然成立,故原命题成立.
证法二:设y=![]() ,则(y-1)x2+(y+1)x+y-1=0.
,则(y-1)x2+(y+1)x+y-1=0.
①当y=1时![]() x=0.
x=0.
②当y≠1时,上式是关于x的二次方程,一定有实数解.
∴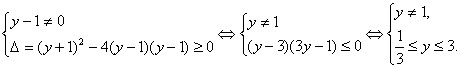
综合①得![]() ≤y≤3,
≤y≤3,
即![]() ≤
≤![]() ≤3.
≤3.
证法三:y=![]() =1-
=1-![]() .
.
①当x=0时,y=1.
②当x>0时, ![]() =
=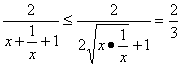 .
.
∴1>y≥1-![]() =
=![]() .
.
③当x<0时,![]() =
=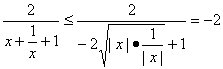 .
.
∴1<y≤1-(-2)=3.
总之,![]() ≤y≤3.
≤y≤3.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
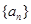 中,
中, ,其前
,其前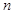 项和
项和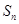 满足:
满足: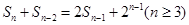 ,令
,令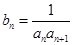 .
.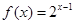 ,求证:
,求证: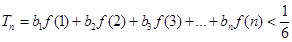 ;
;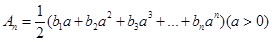 ,问是否存在正实数
,问是否存在正实数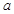 同时满足下列两个条件?
同时满足下列两个条件?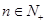 ,都有
,都有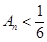 ;
;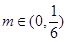 ,均存在
,均存在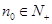 ,使得当
,使得当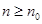 时总有
时总有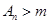 .
.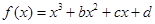 在(-
在(-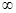 ,0)上是增函数,在[0,2]上是减函数,且方程
,0)上是增函数,在[0,2]上是减函数,且方程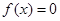 有三个根分别为
有三个根分别为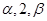 .
.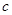 的值;
的值;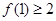 ;
;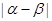 的取值范围.
的取值范围. 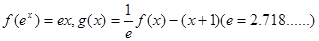
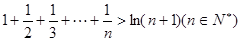
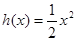 ,曲线y=
,曲线y=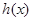 与
y=
与
y=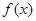 是否存在公共点,若存在公共点,在公共点处是否存在公切线,若存在,求出公切线方程,若不存在,说明理由。
是否存在公共点,若存在公共点,在公共点处是否存在公切线,若存在,求出公切线方程,若不存在,说明理由。