题目内容
已知an=-n2+9n+10(n∈N*)是数列{an}的通项公式.求:(1)数列{an}的最大值;
(2)数列{an}前n项和Sn取最大值时的n.
解:(1)方法一:∵an+1-an=[-(n+1)2+9(n+1)+10]-(-n2+9n+10)=-2(n-4),
当n<4时,an+1>an;
当n>4时,an+1<an;
当n=4时,an+1=an,
即a1<a2<a3<a4=a5>a6>….
∴n=4或n=5时,an最大,此时a4=a5=30.
方法二:an=-n2+9n+10对应函数y=-x2+9x+10(x>0),
其图象的对称轴为x=![]() ,易确定n=4或n=5时,an最大,最大值为30.
,易确定n=4或n=5时,an最大,最大值为30.
(2)∵an对应函数y=-x2+9x+10,当y≥0时有-1≤x≤10,
∴当1≤n≤10时,an≥0;当n>10时,an<0,
即有S1<S2<S3<…<S9=S10>S11>S12>…,
故Sn取到最大值时的n为9或10.

练习册系列答案
相关题目
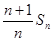
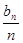 的最小值.
的最小值.