Question

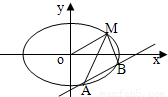
已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的2倍，且经过点M（2，1），平行于OM直线?在y轴上的截距为m（m＜0），设直线?交椭圆于两个不同点A、B，
（1）求椭圆方程；
（2）求证：对任意的m的允许值，△ABM的内心I在定直线x=2上．

Answer 1

【答案】分析：（1）设出椭圆的标准方程，利用长轴长是短轴长的2倍，且经过点M（2，1），建立方程组，从而可求椭圆的方程；
（2）证明△ABM的角平分线MI垂直x轴，从而内心I的横坐标等于点M的横坐标，则可得对任意的m的允许值，△ABM的内心I在定直线 x=2上．
解答：（1）解：设椭圆方程为
则∵长轴长是短轴长的2倍，且经过点M（2，1），
∴
所以，椭圆方程为（5分）
（2）证明：因为直线?平行于OM，且在y轴上的截距为m，又，所以直线?的方程为，
由，
设A（x₁，y₁），B（x₂，y₂），则，（8分）
设直线MA、MB的斜率分别为k₁、k₂，则，
故===（12分）
故k₁+k₂=0，所以，△ABM的角平分线MI垂直x轴，因此，内心I的横坐标等于点M的横坐标，则对任意的m的允许值，△ABM的内心I在定直线 x=2上（13分）
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，解题的关键是联立方程组，利用韦达定理，从而确定直线MA、MB的斜率的和为0．