题目内容
6.已知实数X,Y满足:$\left\{\begin{array}{l}x-2y+1≥0\\ x<2\\ x+y-1≥0\end{array}\right.$,z=|2x-2y-1|,则z的取值范围是[0,5).分析 先画出可行域,再把目标函数变形为直线的斜截式,根据其在y轴上的截距即可求之.
解答 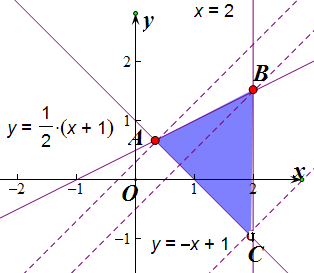 解:画出可行域,如图所示解得A($\frac{1}{3}$,$\frac{2}{3}$),C(2,-1)
解:画出可行域,如图所示解得A($\frac{1}{3}$,$\frac{2}{3}$),C(2,-1)
把设z=|t|,则t=2x-2y-1
t=2x-2y-1变形为y=x-$\frac{1}{2}$t$-\frac{1}{2}$,则直线经过点A时t取得最小值;则直线经过点C时t取得最大,
所以tmin=2×$\frac{1}{3}$-2×$\frac{2}{3}$-1=-$\frac{5}{3}$,tmax=2×2-2×(-1)-1=5
∴z的取值范围为[0,5)
故答案为:[0,5).
点评 本题主要考查线性规划的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
17.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{PF}$=3$\overrightarrow{QF}$,则|QF|=( )
| A. | $\frac{5}{2}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | 6 |
16.如图所示,程序框图的功能是( )


| A. | 求{$\frac{1}{n}$}前10项和 | B. | 求{$\frac{1}{2n}$}前10项和 | C. | 求{$\frac{1}{n}$}前11项和 | D. | 求{$\frac{1}{2n}$}前11项和 |