题目内容
设函数f(x)=sinx+sin(x+ ).
).
(1)求f(x)的最小值,并求使f(x)取得最小值的x的集合;
(2)不画图,说明函数y=f(x)的图像可由y=sinx的图像经过怎样的变化得到.
(1)因为f(x)=sinx+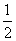 sinx+
sinx+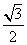 cosx
cosx
= sinx+
sinx+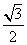 cosx=
cosx=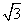 sin(x+
sin(x+ ).
).
所以当x+ =2kπ-
=2kπ- ,即x=2kπ-
,即x=2kπ- (k∈Z)时,f(x)取最小值-
(k∈Z)时,f(x)取最小值-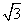 .
.
此时x的取值集合为{x|x=2kπ- ,k∈Z}.
,k∈Z}.
(2)先将y=sinx的图像上所有点的纵坐标伸长到原来的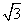 倍(横坐标不变),得y=
倍(横坐标不变),得y=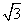 sinx的图像;再将y=
sinx的图像;再将y=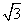 sinx的图像上所有的点向左平移
sinx的图像上所有的点向左平移 个单位,得y=f(x)的图像.
个单位,得y=f(x)的图像.

练习册系列答案
相关题目
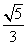 且α∈(-
且α∈(-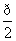 ,0),则sin(π-α)=( )
,0),则sin(π-α)=( )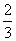
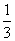 D.±
D.± ,α是第三象限的角,则sin(α+
,α是第三象限的角,则sin(α+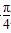 )=( )
)=( )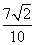 B.
B. D.
D.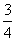 π<α<π,tanα+
π<α<π,tanα+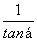 =-
=-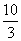 .
.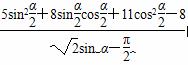 的值.
的值.

 =________.
=________.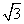 ,则c=( )
,则c=( )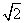 D.1
D.1 B.
B.
 D.
D.