题目内容
下列命题不正确的是（ ）
| A．若如果一个平面内的一条直线垂直于另一个平面内的任意直线，则两平面垂直 |
| B．若一个平面内的任一条直线都平行于另一个平面，则两平面平行 |
| C．若一条直线和一个平面平行，经过这条直线的平面和这个平面相交，则这条直线和交线平行 |
| D．若两条不同的直线在一平面内的射影互相垂直，则这两条直线垂直 |
D
解析试题分析：A选项是直线与平面垂直的定义.B选项是直线与平面平行的定义.由一条直线和一个平面平行，及该直线不在平面内，又因为经过这条直线的平面和这个平面相交，由直线与平面的性质定理可得，这条直线和交线平行.选项D两直线也可以不垂直.所以选B.本题主要是考察线面垂直、面面平行的判定和直线与平面平行的性质.对这些定理要理解清楚.
考点：1.线面垂直的判定定理.2.面面平行的判定定理.3.线面平行的性质定理.
练习册系列答案
阅读快车系列答案
相关题目
关于直线
及平面
，下列命题中正确的是（ ）
A． | B． |
C． | D． |
已知直线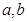
都在平面
外, 则下列推断错误的是（ ）
A． | B． |
C． | D． |
给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中，为真命题的是 （ ）
| A．①和② | B．②和③ | C．③和④ | D．②和④ |
在正方体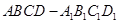
中，异面直线
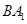与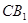
所成的角为（ ）
A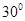． | B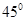． | C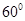． | D． |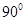
已知
为异面直线,
平面
,
平面
.直线
满足
,则( )
A． ,且 |
B． ,且 |
| C．与相交,且交线垂直于 |
| D．与相交,且交线平行于 |
在空间直角坐标系中，点
，关于
轴对称的点的坐标是( )
A． | B． | C． | D． |
已知直线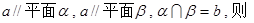 
与
（ ）
| A．相交 | B．平行 | C．异面 | D．共面或异面 |
设
为直线，
是两个不同的平面，下列命题中正确的是（ ）
A．若 ，则 | B．若 ，则 |
C．若 ，则 | D．若 ，则 |