Question

【题目】如图，在多面体中，为矩形，为等腰梯形，，，，且，平面平面，，分别为，的中点.

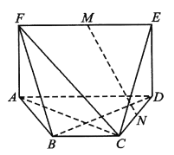
（Ⅰ）求证：平面；

（Ⅱ）若，求多面体的体积.

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）.

【解析】

（Ⅰ）取的中点.连接，，可证，，然后利用平面平面，可证平面.（Ⅱ）将多面体分为四棱锥和三棱锥两部分，将转化为，然后利用四棱锥和三棱锥的体积公式分别求出然后求和即可.

解：（Ⅰ）如图，取的中点.连接，.

在矩形中，∵，分别为线段，的中点，

∴.

又平面，平面，

∴平面.

在中，∵，分别为线段，的中点，

∴.

又平面，平面，

∴平面.

又，平面，

∴平面平面

又平面，∴平面.

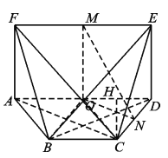
（Ⅱ）如图，过点作于.

∵平面平面，平面平面，平面，

∴平面.

同理平面.

连接，.在中，∵，，

∴.

同理.

∵，∴等边的高为，即.

连接.

∴

.