题目内容
设整数n≥4,P(a,b) 是平面直角坐标系xOy 中的点,其中a,b∈{1,2,3,…,n},a>b.(1)记An 为满足a-b=3 的点P 的个数,求An;
(2)记Bn 为满足
| 1 | 3 |
分析:(1)An 为满足a-b=3 的点P 的个数,显然P(a,b)的坐标的差值,与An中元素个数有关,直接写出An的表达式即可.
(2)设k为正整数,记fn(k)为满足题设条件以及a-b=3k的点P的个数,讨论fn(k)≥1的情形,推出fn(k)=n-3k,根据k的范围k ≤
,说明n-1是3的倍数和余数,
然后求出Bn.
(2)设k为正整数,记fn(k)为满足题设条件以及a-b=3k的点P的个数,讨论fn(k)≥1的情形,推出fn(k)=n-3k,根据k的范围k ≤
| n-1 |
| 3 |
然后求出Bn.
解答:解:(1)点P的坐标中,满足条件:1≤b=a-3≤n-3,所以An=n-3;
(2)设k为正整数,记fn(k)为满足题设条件以及a-b=3k的点P的个数,只要讨论fn(k)≥1的情形,由1≤b=a-3k≤n-3k,
知fn(k)=n-3k且k ≤
,设n-1=3m+r,其中m∈N+,r∈{0,1,2},则k≤m,所以
Bn=
fn(k)=
(n-3k)=mn-
=
将m=
代入上式,化简得Bn=
-
所以Bn=
(2)设k为正整数,记fn(k)为满足题设条件以及a-b=3k的点P的个数,只要讨论fn(k)≥1的情形,由1≤b=a-3k≤n-3k,
知fn(k)=n-3k且k ≤
| n-1 |
| 3 |
Bn=
| m |
 |
| k=1 |
| m |
 |
| k=1 |
| 3m(m+1) |
| 2 |
| m(2n-3m-3) |
| 2 |
将m=
| n-1-r |
| 3 |
| (n-1)(n-2) |
| 6 |
| r(r-1) |
| 6 |
所以Bn=
|
点评:本题是难题,考查数列通项公式的求法,数列求和的方法,考查发现问题解决问题的能力,解题中注意整除知识的应用,转化思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。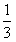 (a-b)是整数的点P的个数,求Bn。
(a-b)是整数的点P的个数,求Bn。 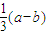 是整数的点P 的个数,求Bn.
是整数的点P 的个数,求Bn.