Question

【题目】如图，已知四棱台上、下底面分别是边长为3和6的正方形，，且
底面，点，分别在棱，上.
(1)若是是的中点，证明：;
(2若//平面，二面角的余弦值为，求四面体的体积

Answer 1

【答案】由题意得， A A 1 , A B , A D 两两垂直，以 A 为坐标原点， A B , A D , A A 1 所在直线分别为 x 轴 y 轴 z 轴,建立如图下图所示的空间直角坐标系，则相关各点的坐标为 A ( 0 , 0 , 0 ) , B 1 ( 3 , 0 , 6 ) , D ( 0 , 6 , 0 ) , D 1 ( 0 , 3 , 6 ) , Q ( 6 , m , 0 ) , 其中 m = B Q , 0 ≤ m ≤ 6 .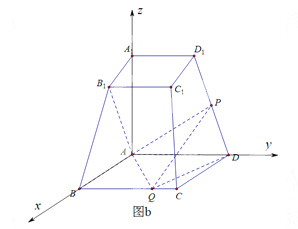

（1）若是的中点，则于是所以.即
（2）由题意设知，是平面内的两个不共线向量.设是平面的一个法向量，则即,取得,又平面的一个法向量所以
而二面角P-QD-A的余弦值为 ， 因此=解得.m=4或者m=8（舍去）此时Q（6,4,0）设而=(0，-3，6)由此得点P因为PQ//平面ABB1A1且平面ABB1A1的一个法向量=(0,1,0)所以，·=0即，亦即得从而P（0,4,4,）于是将四面体ADPQ视为以ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积




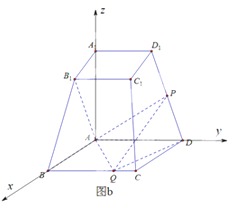
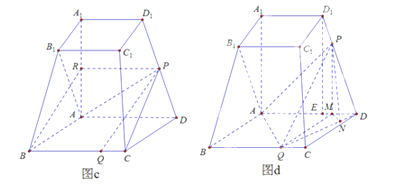
【解析】由题意得，两两垂直，以为坐标原点，所在直线分别为轴轴轴,建立如图下图所示的空间直角坐标系，则相关各点的坐标为其中.

（1）若是的中点，则于是所以.即
（2）由题意设知，是平面内的两个不共线向量.设是平面的一个法向量，则即,取得,又平面的一个法向量所以
而二面角P-QD-A的余弦值为，因此=解得.m=4或者m=8（舍去）此时Q（6,4,0）设而=(0，-3，6)由此得点P因为PQ//平面ABB1A1且平面ABB1A1的一个法向量=(0,1,0)所以，·=0即，亦即得从而P（0,4,4,）于是将四面体ADPQ视为以ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积




【考点精析】通过灵活运用向量的三角形法则和平面向量的坐标运算，掌握三角形加法法则的特点：首尾相连;三角形减法法则的特点：共起点，连终点，方向指向被减向量；坐标运算：设，则;;设，则即可以解答此题．