题目内容
已知曲线
+
=1,当m∈[-2,-1]时,该曲线的离心率e的取值范围是
| x2 |
| 4 |
| y2 |
| m |
[
,
]
| ||
| 2 |
| ||
| 2 |
[
,
]
.
| ||
| 2 |
| ||
| 2 |
分析:方程即
-
=1,由 a=2,b=
∈[1,
],∴c=
∈[
,
],求出e=
的范围.
| x2 |
| 4 |
| y2 |
| -m |
| -m |
| 2 |
| 4-m |
| 5 |
| 6 |
| c |
| a |
解答:解:曲线
+
=1,当m∈[-2,-1]时,方程即
-
=1,
a=2,b=
∈[1,
],∴c=
∈[
,
].
∴e=
∈[
,
],
故答案为:[
,
].
| x2 |
| 4 |
| y2 |
| m |
| x2 |
| 4 |
| y2 |
| -m |
a=2,b=
| -m |
| 2 |
| 4-m |
| 5 |
| 6 |
∴e=
| c |
| a |
| ||
| 2 |
| ||
| 2 |
故答案为:[
| ||
| 2 |
| ||
| 2 |
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,把方程化为标准形式,是解题的突破口.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
已知二次曲线
+
=1,当离心率e∈[
,?
]时,则实数λ的取值范围是( )
| x2 |
| 4 |
| y2 |
| λ |
| ||
| 2 |
| ||
| 2 |
| A、[-2,?0] |
| B、[-3,?1] |
| C、[-2,?-1] |
| D、[-2,?-1] |
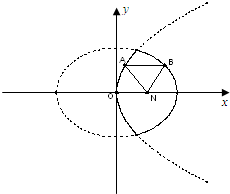 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆