题目内容
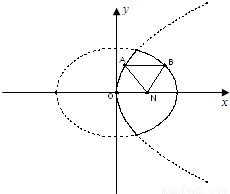
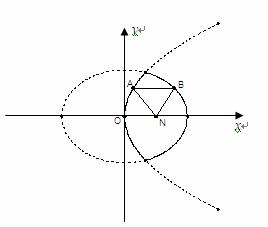
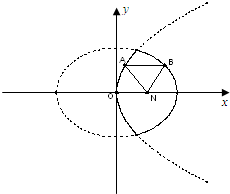 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆| x2 |
| 4 |
| y2 |
| 3 |
[文]点P是曲线y=x2-lnx上任意一点,则P到直线y=x-2的距离的最小值是
分析:[理]先根据抛物线方程和椭圆方程分别求得他们的准线方程,设出A,B的坐标,过A作AH垂直x=-1 BI垂直x=4,根据抛物线和椭圆的定义求得|NA|=|AH|=x1+1,|NB|=|BH|•
=
,进而表示出三角形周长,化简整理后,求得周长L关于x2的表达式,联立抛物线和椭圆方程求得两曲线的交点,判断出x2的范围,进而确定L的范围.
[文]由题意知,当曲线上过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小.求出曲线对应的函数的导数,令导数值等于1,可得且点的坐标,此切点到直线y=x-2的距离即为所求.
| 1 |
| 2 |
| 4-x2 |
| 2 |
[文]由题意知,当曲线上过点P的切线和直线y=x-2平行时,点P到直线y=x-2的距离最小.求出曲线对应的函数的导数,令导数值等于1,可得且点的坐标,此切点到直线y=x-2的距离即为所求.
解答:解:[理]依题意可知抛物线准线为x=-1
椭圆右准线为x=4
设A(x1,y) B(x2,y)
过A作AH垂直x=-1 BI垂直x=4
由圆锥曲线第二定义
|NA|=|AH|=x1+1
|NB|=|BH|•
=
L=x1+1+x2-x1+
=
联立抛物线和椭圆方程求得x=
或-6(舍负)
∴
≤x2≤2
∴
≤
≤4
即L的取值范围是(
,4)
[文]点P是曲线y=x2-lnx上任意一点,
当过点P的切线和直线y=x-2平行时,
点P到直线y=x-2的距离最小.
直线y=x-2的斜率等于1,
令y=x2-lnx的导数 y′=2x-
=1,x=1,或 x=-
(舍去),
故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于
,
故点P到直线y=x-2的最小距离为
,
故答案为:(
,4),
椭圆右准线为x=4
设A(x1,y) B(x2,y)
过A作AH垂直x=-1 BI垂直x=4
由圆锥曲线第二定义
|NA|=|AH|=x1+1
|NB|=|BH|•
| 1 |
| 2 |
| 4-x2 |
| 2 |
L=x1+1+x2-x1+
| 4-x2 |
| 2 |
| x2+6 |
| 2 |
联立抛物线和椭圆方程求得x=
| 2 |
| 3 |
∴
| 2 |
| 3 |
∴
| 10 |
| 3 |
| x2+6 |
| 2 |
即L的取值范围是(
| 10 |
| 3 |
[文]点P是曲线y=x2-lnx上任意一点,
当过点P的切线和直线y=x-2平行时,
点P到直线y=x-2的距离最小.
直线y=x-2的斜率等于1,
令y=x2-lnx的导数 y′=2x-
| 1 |
| x |
| 1 |
| 2 |
故曲线y=x2-lnx上和直线y=x-2平行的切线经过的切点坐标(1,1),
点(1,1)到直线y=x-2的距离等于
| 2 |
故点P到直线y=x-2的最小距离为
| 2 |
故答案为:(
| 10 |
| 3 |
| 2 |
点评:本题主要考查了椭圆和抛物线的应用,点到直线的距离公式的应用,函数的导数的求法及导数的意义,体现了转化的数学思想.

练习册系列答案
相关题目

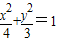 的实线上运动,若AB∥x轴,点N的坐标为(1,0),则△ABN的周长l的取值范围是 .
的实线上运动,若AB∥x轴,点N的坐标为(1,0),则△ABN的周长l的取值范围是 .