题目内容
【题目】已知△ABC的内角A，B，C所对的边分别为
，b，c，且，b，c成等比数列，
.
（1）求
的值；
（2）若△ABC的面积为2，求△ABC的周长．
【答案】(1) 
(2) 
【解析】
（1）首先根据题意可知
，根据正弦定理转化为
，再变形
，代入求值；
（2）首先根据面积求
，再根据余弦定理求
.
解：(1)△ABC中，∵cosB=
＞0，∴sinB=
由a，b，c成等比数列，得b2=ac，根据正弦定理得：sin2B=sinAsinC，
∴
=
=
=
；
(2)△ABC的面积为S△ABC=
acsinB=b2
=2，∴b=
；
由余弦定理b2=a2+c2﹣2accosB=a2+c2﹣2×5×，
∴a2+c2=b2+6=5+5=11，∴（a+c）2=a2+2ac+c2=11+2×5=21，
∴
；∴△ABC的周长为a+b+c=
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
【题目】武汉某科技公司为提高市场销售业绩，现对某产品在部分营销网点进行试点促销活动．现有两种活动方案，在每个试点网点仅采用一种活动方案，经统计，2018年1月至6月期间，每件产品的生产成本为10元，方案1中每件产品的促销运作成本为5元，方案2中每件产品的促销运作成本为2元，其月利润的变化情况如图①折线图所示．
（1）请根据图①，从两种活动方案中，为该公司选择一种较为有利的活动方案（不必说明理由）；
（2）为制定本年度该产品的销售价格，现统计了8组售价xi（单位：元/件）和相应销量y（单位：件）（i＝1，2，…8）并制作散点图（如图②），观察散点图可知，可用线性回归模型拟合y与x的关系，试求y关于x的回归方程（系数精确到整数）；
参考公式及数据：
40，
660，
xiyi＝206630，x
12968，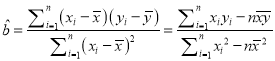
，
，
（3）公司策划部选
1200lnx+5000和
═
x3+1200两个模型对销量与售价的关系进行拟合，现得到以下统计值（如表格所示）：
|
| |
| 52446.95 | 122.89 |
| 124650 | |
相关指数 | R | R |
相关指数：R2＝1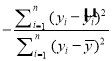
．
（i）试比较R12，R22的大小（给出结果即可），并由此判断哪个模型的拟合效果更好；
（ii）根据（1）中所选的方案和（i）中所选的回归模型，求该产品的售价x定为多少时，总利润z可以达到最大？