题目内容
 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船.
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船.(Ⅰ)求处于C处的乙船和遇险渔船间的距离;
(Ⅱ)设乙船沿直线CB方向前往B处救援,其方向与
 成θ角,求f(x)=sin2θsinx+cos2θcosx(x∈R)的值域.
成θ角,求f(x)=sin2θsinx+cos2θcosx(x∈R)的值域.
【答案】分析:(Ⅰ)连接BC,依题意可知AC,AB的值和∠CAB,进而由余弦定理求得BC.
(Ⅱ)先根据正弦定理求得sinθ,进而根据同角三角函数基本关系求得cosθ,进而利用两角和公式化简函数的解析式,进而根据正弦函数的性质求得函数的值域.
解答: 解:(Ⅰ)连接BC,由余弦定理得BC2=202+102-2×20×10COS120°=700.
解:(Ⅰ)连接BC,由余弦定理得BC2=202+102-2×20×10COS120°=700.
∴BC=10 .
.
(Ⅱ)∵ ,
,
∴sinθ=
∵θ是锐角,
∴ ,
,
f(x)=sin2θsinx+cos2θcosx=
∴f(x)的值域为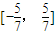 .
.
点评:本题主要考查了解三角形中的实际运用.考查了学生运用所学知识解决实际问题的能力.
(Ⅱ)先根据正弦定理求得sinθ,进而根据同角三角函数基本关系求得cosθ,进而利用两角和公式化简函数的解析式,进而根据正弦函数的性质求得函数的值域.
解答:
 解:(Ⅰ)连接BC,由余弦定理得BC2=202+102-2×20×10COS120°=700.
解:(Ⅰ)连接BC,由余弦定理得BC2=202+102-2×20×10COS120°=700.∴BC=10
 .
.(Ⅱ)∵
 ,
,∴sinθ=

∵θ是锐角,
∴
 ,
,f(x)=sin2θsinx+cos2θcosx=

∴f(x)的值域为
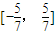 .
.点评:本题主要考查了解三角形中的实际运用.考查了学生运用所学知识解决实际问题的能力.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
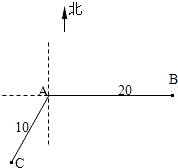 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船.
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船.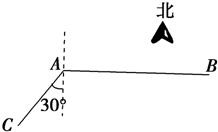 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,乙船立即朝北偏东θ角的方向沿直线前往B处救援,则sinθ的值等于( )
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,乙船立即朝北偏东θ角的方向沿直线前往B处救援,则sinθ的值等于( ) 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,乙船立即朝北偏东θ角的方向沿直线前往B处救援,则sinθ的值等于
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,乙船立即朝北偏东θ角的方向沿直线前往B处救援,则sinθ的值等于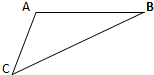 中新社亚丁湾2011年2月5日电,中国海军第七批护航编队采取直升机低空查证、发射爆震弹示警等措施,成功驱离多艘小艇,如图,当甲船位于A处时,在其正东方向相距20海里的B处有一艘货船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,乙船立即朝北偏东θ角的方向沿直线前往B处救援,求sinθ的值.
中新社亚丁湾2011年2月5日电,中国海军第七批护航编队采取直升机低空查证、发射爆震弹示警等措施,成功驱离多艘小艇,如图,当甲船位于A处时,在其正东方向相距20海里的B处有一艘货船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,乙船立即朝北偏东θ角的方向沿直线前往B处救援,求sinθ的值.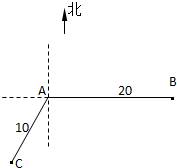 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救、甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船.
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救、甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船.