Question

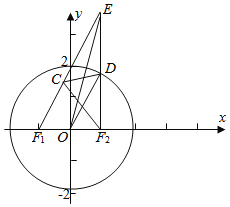
【题目】已知圆O；x2+y2=4，F1（-1，0），F2（1，0），点D圆O上一动点，2=，点C在直线EF1上，且=0，记点C的轨迹为曲线W．

（1）求曲线W的方程；

（2）已知N（4，0），过点N作直线l与曲线W交于A，B不同两点，线段AB的中垂线为l'，线段AB的中点为Q点，记P与y轴的交点为M，求|MQ|的取值范围．

Answer 1

【答案】（1）； （2）[0，5）.

【解析】

（1）由题，易知点D是的中点，可得CE=CF2即CF1+CF2=4为定值，可得C的轨迹为以（-1，0），（1，0）为焦点的椭圆；

（2）由题，设直线l的方程，联立椭圆，求得点N的坐标（注意考虑判别式），再得出l'的直线方程，再求得点M的坐标，即可求得MQ的长度，求出其范围即可.

（1）圆O：x2+y2=4，圆心为（0，0），半径r=4，

F1（-1，0），F2（1，0），点D是圆O上一动点，

由2=，可得D为EF2的中点，

点C在直线EF1上，且=0，可得CD⊥EF2，

连接CF2，可得CE=CF2，

且CF1+CF2=CF1+CE=EF1=2OD=4，

由椭圆的定义可得，C的轨迹为以（-1，0），（1，0）为焦点的椭圆，

可得c=1，a=2，b==，

则曲线W的方程为；

（2）由题意可知直线l的斜率存在，

设l：y=k（x-4），A（x1，y1），B（x2，y2），Q（x0，y0），

联立直线与椭圆方程3x2+4y2=12，消去y得：

（3+4k2）x2-32k2x+64k2-12=0，

x1+x2=，x1x2=，

又△=（-32k2）2-4（3+4k2）（64k2-12）＞0，解得-＜k＜，

x0==，y0=k（x0-4）=-，

∴Q（，-），

∴l'：y-y0=-（x-x0），即y+=-（x-），

化简得y=-x+，

令x=0，得m=，即M（0，），

|MQ|=（）2+（）2=256，

令t=3+4k2，则t∈[3，4），

∴|MQ|=256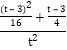=16=16[-3（）2-+1]=16[-3（）2+]．

∴|MQ|∈[0，5）

．