题目内容
若 ,则f(x)=________.
,则f(x)=________.
2x2-4x+3(x≥1)
分析:本题可用换元法,令 ,然后解出x,把等式右侧的x代入后整理可得f(t)的表达式,即可求出函数f(x)的解析式.
,然后解出x,把等式右侧的x代入后整理可得f(t)的表达式,即可求出函数f(x)的解析式.
解答:令 (t≥1),则x=(t-1)2,
(t≥1),则x=(t-1)2,
所以原式变为f(t)=2(t-1)2+1=2t2-4t+3(t≥1)
即f(x)=2x2-4x+3(x≥1).
故答案为2x2-4x+3(x≥1).
点评:本题考查了函数解析式的求解及常用方法,考查了换元法,运用换元法求函数解析式时注意定义域.
分析:本题可用换元法,令
 ,然后解出x,把等式右侧的x代入后整理可得f(t)的表达式,即可求出函数f(x)的解析式.
,然后解出x,把等式右侧的x代入后整理可得f(t)的表达式,即可求出函数f(x)的解析式.解答:令
 (t≥1),则x=(t-1)2,
(t≥1),则x=(t-1)2,所以原式变为f(t)=2(t-1)2+1=2t2-4t+3(t≥1)
即f(x)=2x2-4x+3(x≥1).
故答案为2x2-4x+3(x≥1).
点评:本题考查了函数解析式的求解及常用方法,考查了换元法,运用换元法求函数解析式时注意定义域.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
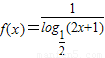 ,则f(x)的定义域为( )
,则f(x)的定义域为( )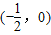
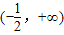
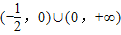
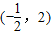
 ,则f(x)的定义域为( )
,则f(x)的定义域为( )



 ,则F(x)的最大值为 .
,则F(x)的最大值为 . ,则f(x)的定义域为( )
,则f(x)的定义域为( )



 ,则F(x)的最大值为 .
,则F(x)的最大值为 .