题目内容
已知函数 ,
,  .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当 时,函数
时,函数 在
在 上的最大值为
上的最大值为 ,若存在
,若存在 ,使得
,使得 成立,求实数b的取值范围.
成立,求实数b的取值范围.
 ,
,  .
. (Ⅰ)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(Ⅱ)当
 时,求函数
时,求函数 的单调区间;
的单调区间; (Ⅲ)当
 时,函数
时,函数 在
在 上的最大值为
上的最大值为 ,若存在
,若存在 ,使得
,使得 成立,求实数b的取值范围.
成立,求实数b的取值范围.(Ⅰ)曲线 在点
在点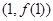 处的切线方程
处的切线方程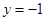 。
。
(Ⅱ)函数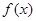 的递增区间为
的递增区间为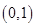 ,递减区间为
,递减区间为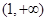 。
。
(Ⅲ)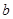 的取值范围是
的取值范围是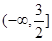 .
.
 在点
在点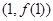 处的切线方程
处的切线方程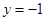 。
。(Ⅱ)函数
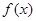 的递增区间为
的递增区间为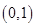 ,递减区间为
,递减区间为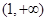 。
。(Ⅲ)
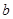 的取值范围是
的取值范围是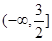 .
. 试题分析:(Ⅰ)当
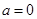 时,
时,
 1分
1分
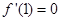 .2分
.2分所以曲线
 在点
在点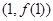 处的切线方程
处的切线方程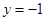 3分
3分(Ⅱ)
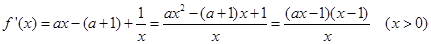 4分
4分当
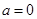 时,解
时,解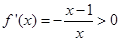 ,得
,得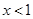 ,解
,解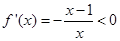 ,得
,得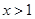
所以函数
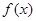 的递增区间为
的递增区间为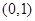 ,递减区间为在
,递减区间为在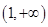 5分
5分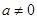 时,令
时,令 得
得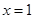 或
或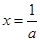
ⅰ)当
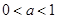 时,
时,
| x | 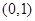 ) ) | 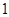 |  |  |  |
| f’(x) | + | | - | | + |
| f(x) | 增 | | 减 | | 增 |
函数
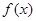 的递增区间为
的递增区间为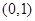 ,
,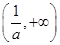 ,递减区间为
,递减区间为 7分
7分ⅱ)当
 时,
时,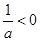
在
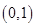 上
上 ,在
,在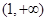 上
上 8分
8分函数
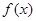 的递增区间为
的递增区间为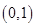 ,递减区间为
,递减区间为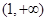 9分
9分(Ⅲ)由(Ⅱ)知,当
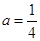 时,
时,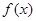 在
在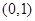 上是增函数,在
上是增函数,在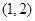 上是减函数,
上是减函数,所以
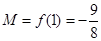 , 11分
, 11分存在
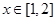 ,使
,使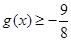 即存在
即存在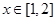 ,使
,使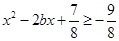 ,
,方法一:只需函数
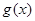 在[1,2]上的最大值大于等于
在[1,2]上的最大值大于等于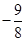
所以有
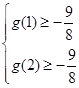 即
即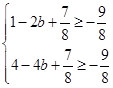 解得:
解得: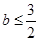 13分
13分方法二:将
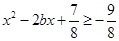 整理得
整理得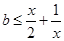
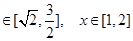
从而有
 所以
所以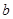 的取值范围是
的取值范围是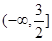 . 13分
. 13分点评:中档题,本题属于导数应用中的常见问题,通过研究函数的单调性,明确最值情况。曲线切线的斜率,等于函数在切点处的导函数值。在给定区间,如果函数的导数非负,则函数为增函数,如果函数的导数非正,则函数为减函数。涉及不等式恒成立问题,往往通过构造函数,研究函数的最值,得到确定参数(范围)的目的。对数函数要注意其真数大于0.

练习册系列答案
相关题目
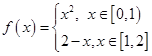 ,则
,则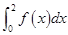 的值为( )
的值为( )



 与曲线
与曲线 相切,则
相切,则 的值为 .
的值为 . 的图像在点(2,8)处的切线与第四象限围成三角形的面积为______________
的图像在点(2,8)处的切线与第四象限围成三角形的面积为______________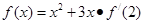 ,则
,则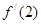 =
=  在D上可导,即
在D上可导,即 存在,且导函数
存在,且导函数 =
= ,若
,若 上不是凸函数的是( )
上不是凸函数的是( ) 



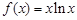 .
. 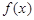 的最小值;
的最小值;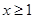 都有
都有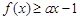 ,求实数
,求实数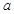 的取值范围.
的取值范围.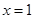 是有极大值4,当
是有极大值4,当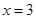 是有极小值0,且函数过原点,则此函数是( )
是有极小值0,且函数过原点,则此函数是( )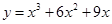
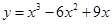
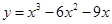
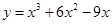
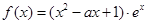 .
.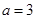 时,求曲线
时,求曲线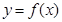 在点
在点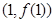 处的切线方程;
处的切线方程; ,
,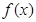 在区间
在区间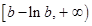 上是增函数,求实数
上是增函数,求实数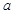 的取值范围.
的取值范围.