题目内容
在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率分别为
、
、
、
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率.
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率.
分析:(Ⅰ)根据题意,设事件Ai(i=1,2,3,4)表示“该选手能正确回答第i轮问题”,设事件B表示“该选手进入第三轮被淘汰”,事件B即A1、A2发生,且
发生,由独立事件概率的乘法公式,计算可得答案;
(Ⅱ)设事件C表示“该选手至多进入第三轮考核”,包含三个基本事件,即第一轮被淘汰、第二轮被淘汰、第三轮被淘汰,由互斥事件的概率公式,计算可得答案.
. |
| A3 |
(Ⅱ)设事件C表示“该选手至多进入第三轮考核”,包含三个基本事件,即第一轮被淘汰、第二轮被淘汰、第三轮被淘汰,由互斥事件的概率公式,计算可得答案.
解答:解:设事件Ai(i=1,2,3,4)表示“该选手能正确回答第i轮问题”.
由已知P(A1)=
,P(A2)=
,P(A3)=
,P(A4)=
.
(Ⅰ)设事件B表示“该选手进入第三轮被淘汰”,
事件B即该选手正确回答的第一、二轮的问题,而第三轮问题回答错误,
则P(B)=P(A1A2
)=
×
×(1-
)=
,
(Ⅱ)设事件C表示“该选手至多进入第三轮考核”,
包含三个基本事件,即第一轮被淘汰、第二轮被淘汰、第三轮被淘汰,
则P(C)=P(
+A1
+A1A2
)=
+
×
+
×
×(1-
)=
.
由已知P(A1)=
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
(Ⅰ)设事件B表示“该选手进入第三轮被淘汰”,
事件B即该选手正确回答的第一、二轮的问题,而第三轮问题回答错误,
则P(B)=P(A1A2
. |
| A3 |
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 6 |
(Ⅱ)设事件C表示“该选手至多进入第三轮考核”,
包含三个基本事件,即第一轮被淘汰、第二轮被淘汰、第三轮被淘汰,
则P(C)=P(
. |
| A1 |
. |
| A2 |
. |
| A3 |
| 1 |
| 6 |
| 5 |
| 6 |
| 1 |
| 5 |
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 2 |
点评:本题考查互斥事件、相互独立事件的概率计算,注意分析事件之间的关系,选择对应的公式进行计算.

练习册系列答案
相关题目
 、
、 、
、 、
、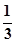 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.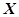 ,求随机变量
,求随机变量 、
、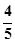 、
、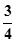 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。 、
、 、
、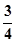 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。