题目内容
已知P是曲线xy-x-y=1上任意一点,O为坐标原点,则|OP|的最小值为( )
A、6-4
| ||
B、2-
| ||
C、
| ||
| D、1 |
考点:两点间距离公式的应用
专题:计算题,函数的性质及应用
分析:xy-x-y=1可化为(x-1)(y-1)=2,中心在(1,1)的双曲线,根据对称性,令x=y,则x=1±
,即可求出|OP|的最小值.
| 2 |
解答:
解:xy-x-y=1可化为(x-1)(y-1)=2,中心在(1,1)的双曲线,
根据对称性,令x=y,则x=1±
,
∴|OP|的最小值为
(
-1)=2-
,
故选:B.
根据对称性,令x=y,则x=1±
| 2 |
∴|OP|的最小值为
| 2 |
| 2 |
| 2 |
故选:B.
点评:本题考查|OP|的最小值,考查双曲线的性质,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义运算a?b为执行如图所示的程序框图输出的S值,则(2cos
)?tan
的值为( )
| π |
| 3 |
| 7π |
| 4 |

| A、2 | B、-2 | C、-1 | D、1 |
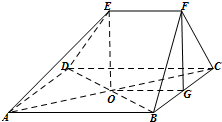 如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.
如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点. 一个几何体的三视图如图所示,则该几何体的体积可能是
一个几何体的三视图如图所示,则该几何体的体积可能是