题目内容
已知圆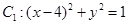 ,圆
,圆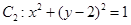 ,动点
,动点 到圆
到圆 ,
,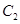 上点的距离的最小值相等.
上点的距离的最小值相等.
(1)求点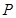 的轨迹方程;
的轨迹方程;
(2)点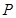 的轨迹上是否存在点
的轨迹上是否存在点 ,使得点
,使得点 到点
到点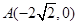 的距离减去点
的距离减去点 到点
到点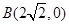 的距离的差为
的距离的差为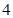 ,如果存在求出
,如果存在求出 点坐标,如果不存在说明理由.
点坐标,如果不存在说明理由.
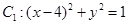 ,圆
,圆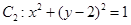 ,动点
,动点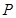 到圆
到圆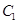 ,
,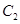 上点的距离的最小值相等.
上点的距离的最小值相等.(1)求点
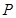 的轨迹方程;
的轨迹方程;(2)点
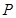 的轨迹上是否存在点
的轨迹上是否存在点 ,使得点
,使得点 到点
到点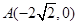 的距离减去点
的距离减去点 到点
到点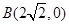 的距离的差为
的距离的差为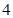 ,如果存在求出
,如果存在求出 点坐标,如果不存在说明理由.
点坐标,如果不存在说明理由.解:(1)设动点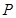 的坐标为
的坐标为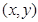 ,
,
圆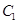 的圆心
的圆心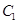 坐标为
坐标为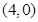 ,圆
,圆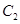 的圆心
的圆心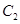 坐标为
坐标为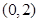 , ……………………2分
, ……………………2分
因为动点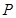 到圆
到圆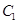 ,
,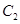 上的点距离最小值相等,所以
上的点距离最小值相等,所以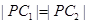 , ……………………3分
, ……………………3分
即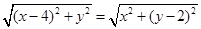 ,化简得
,化简得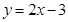 , ……………………4分
, ……………………4分
因此点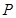 的轨迹方程是
的轨迹方程是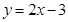 ; ……………………5分
; ……………………5分
(2)假设这样的 点存在,
点存在,
因为 点到
点到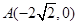 点的距离减去
点的距离减去 点到
点到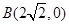 点的距离的差为4,
点的距离的差为4,
所以 点在以
点在以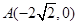 和
和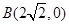 为焦点,实轴长为
为焦点,实轴长为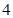 的双曲线的右支上,
的双曲线的右支上,
即 点在曲线
点在曲线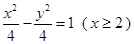 上, ……………………9分
上, ……………………9分
又 点在直线
点在直线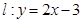 上,
上, 点的坐标是方程组
点的坐标是方程组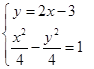 的解,……………………11分
的解,……………………11分
消元得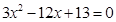 ,
,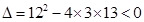 ,方程组无解,
,方程组无解,
所以点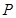 的轨迹上不存在满足条件的点
的轨迹上不存在满足条件的点 . ……………………13分
. ……………………13分
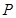 的坐标为
的坐标为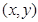 ,
,圆
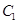 的圆心
的圆心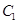 坐标为
坐标为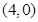 ,圆
,圆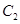 的圆心
的圆心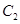 坐标为
坐标为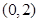 , ……………………2分
, ……………………2分因为动点
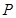 到圆
到圆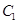 ,
,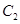 上的点距离最小值相等,所以
上的点距离最小值相等,所以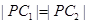 , ……………………3分
, ……………………3分即
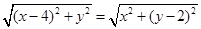 ,化简得
,化简得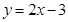 , ……………………4分
, ……………………4分因此点
 的轨迹方程是
的轨迹方程是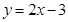 ; ……………………5分
; ……………………5分(2)假设这样的
 点存在,
点存在,因为
 点到
点到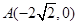 点的距离减去
点的距离减去 点到
点到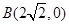 点的距离的差为4,
点的距离的差为4,所以
 点在以
点在以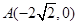 和
和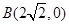 为焦点,实轴长为
为焦点,实轴长为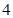 的双曲线的右支上,
的双曲线的右支上,即
 点在曲线
点在曲线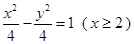 上, ……………………9分
上, ……………………9分又
 点在直线
点在直线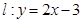 上,
上, 点的坐标是方程组
点的坐标是方程组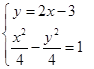 的解,……………………11分
的解,……………………11分消元得
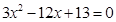 ,
,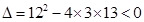 ,方程组无解,
,方程组无解,所以点
 的轨迹上不存在满足条件的点
的轨迹上不存在满足条件的点 . ……………………13分
. ……………………13分略

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
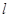 被圆
被圆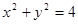 截得的弦长为2,则直线
截得的弦长为2,则直线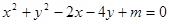 ,
,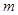 的取值范围;
的取值范围;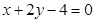 相交于
相交于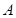 、
、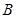 两点,且
两点,且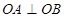 (
(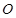 为坐标原点),求
为坐标原点),求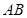 为直径的圆的方程。
为直径的圆的方程。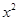 +2
+2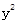 =1与直线xsinθ+y-1=0(θ≠
=1与直线xsinθ+y-1=0(θ≠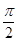 +kπ,k∈Z)的位置关系是
+kπ,k∈Z)的位置关系是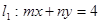 和圆
和圆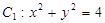 无公共点,则过点
无公共点,则过点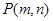 的直线
的直线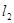 与椭圆
与椭圆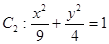 的公共点的个数为( )
的公共点的个数为( ) 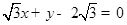 与圆
与圆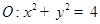 交于
交于 、
、 两点,则
两点,则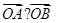 ( )
( )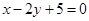 与圆
与圆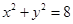 相交于A、B两点,则
相交于A、B两点,则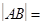 ▲ .
▲ . 直线
直线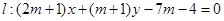 ,
, 恒过的定点;
恒过的定点;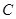 截得的弦长何时最长,何时最短?并求截得的弦长最短时,求
截得的弦长何时最长,何时最短?并求截得的弦长最短时,求 的值以及最短长度。
的值以及最短长度。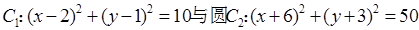 交于A、
交于A、