题目内容
已知数列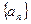 和
和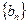 满足:
满足: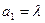 ,
,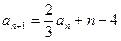 ,
,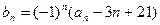 ,其中
,其中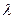 为实数,
为实数,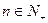 .
.
⑴ 对任意实数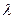 ,证明数列
,证明数列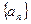 不是等比数列;
不是等比数列;
⑵ 试判断数列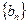 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.
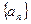 和
和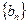 满足:
满足: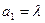 ,
,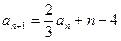 ,
,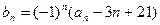 ,其中
,其中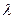 为实数,
为实数,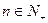 .
.⑴ 对任意实数
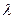 ,证明数列
,证明数列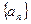 不是等比数列;
不是等比数列;⑵ 试判断数列
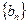 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.证明略
⑴证明数列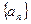 不是等比数列,只需举一个反例;⑵证明数列
不是等比数列,只需举一个反例;⑵证明数列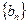 是等比数列,
是等比数列,
常用:①定义法;②中项法.⑴ 证明:假设存在一个实数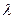 ,使
,使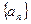 是等比数列,则有
是等比数列,则有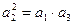 ,
,
即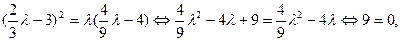 矛盾.
矛盾.
所以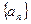 不是等比数列.
不是等比数列.
⑵ 解:因为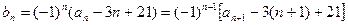
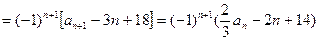
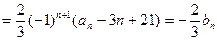
又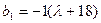 ,所以
,所以
当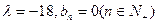 ,此时
,此时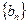 不是等比数列;
不是等比数列;
当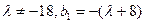 时,由上可知
时,由上可知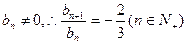 ,此时
,此时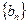 是等比数列.
是等比数列.
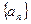 不是等比数列,只需举一个反例;⑵证明数列
不是等比数列,只需举一个反例;⑵证明数列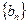 是等比数列,
是等比数列,常用:①定义法;②中项法.⑴ 证明:假设存在一个实数
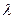 ,使
,使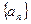 是等比数列,则有
是等比数列,则有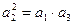 ,
,即
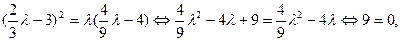 矛盾.
矛盾.所以
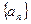 不是等比数列.
不是等比数列. ⑵ 解:因为
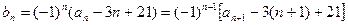
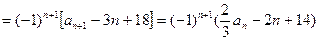
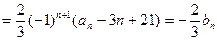
又
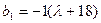 ,所以
,所以当
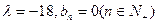 ,此时
,此时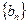 不是等比数列;
不是等比数列;当
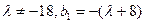 时,由上可知
时,由上可知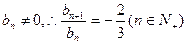 ,此时
,此时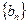 是等比数列.
是等比数列.
练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
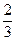 }是等比数列;
}是等比数列;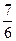 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.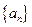 中,
中,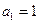 ,
,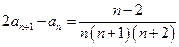 ,
, .
.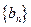 成等比数列; (2)求
成等比数列; (2)求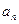 .
.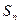 为数列
为数列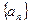 的前
的前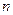 项和,
项和,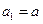 ,
,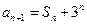 ,
,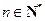 .
.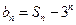 ,求数列
,求数列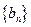 的通项公式;
的通项公式;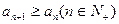 ,求
,求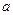 的取值范围.
的取值范围. 为数列
为数列 的前
的前 项和,
项和, 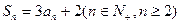 ,求数列
,求数列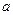 的数列
的数列 既是等差数列,又是等比数列,则这个的前
既是等差数列,又是等比数列,则这个的前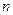 项和
项和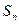 为( )
为( )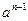
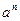
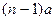
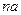
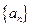 为各项均为正数的等比数列,且
为各项均为正数的等比数列,且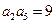 ,则
,则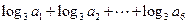 的值为
的值为