题目内容
设二次方程anx2-an+1x+1=0(n=1,2,3,…)有两根α、β,且满足6α-2αβ+6β=3.
(1)试用an表示an+1;
(2)求证:{an-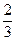 }是等比数列;
}是等比数列;
(3)当a1=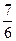 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.
(1)试用an表示an+1;
(2)求证:{an-
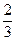 }是等比数列;
}是等比数列;(3)当a1=
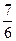 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.(1)根据根与系数的关系,有关系式
代入已知条件6(α+β)-2αβ=3,得 -
- =3.
=3.
∴an+1= an+
an+ .
.
(2)由于an+1= an+
an+ ,改写为an+1-
,改写为an+1-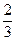 =
= (an-
(an-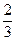 ).
).
故{an-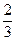 }是等比数列.
}是等比数列.
(3)当a1= 时,a1-
时,a1-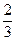 =
= .
.
故{an-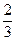 }是以
}是以 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.
∴an=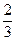 +(
+( )n,n=1,2,3,…,
)n,n=1,2,3,…,
即数列{an}的通项公式是an=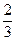 +(
+( )n,n=1,2,3,….
)n,n=1,2,3,….

代入已知条件6(α+β)-2αβ=3,得
 -
- =3.
=3.∴an+1=
 an+
an+ .
.(2)由于an+1=
 an+
an+ ,改写为an+1-
,改写为an+1-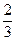 =
= (an-
(an-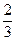 ).
).故{an-
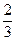 }是等比数列.
}是等比数列.(3)当a1=
 时,a1-
时,a1-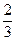 =
= .
.故{an-
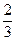 }是以
}是以 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.∴an=
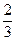 +(
+( )n,n=1,2,3,…,
)n,n=1,2,3,…,即数列{an}的通项公式是an=
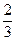 +(
+( )n,n=1,2,3,….
)n,n=1,2,3,….这是有关数列、二次方程的根与系数关系的综合题.根据题目条件列出等量关系,找到递推关系即可求解.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,已知
,已知 ,且
,且 (n∈N*),则
(n∈N*),则 ()
() 中,已知
中,已知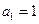 ,
, ,
, .
.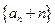 是等比数列;
是等比数列; 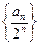 的前项和为
的前项和为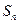 .
.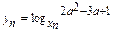 满足
满足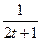 ,yt=
,yt=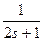 (s,t∈N,且s≠t)共中a为常数,且1<a<
(s,t∈N,且s≠t)共中a为常数,且1<a<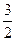 ,试判断,是否存在自然
,试判断,是否存在自然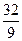 ;
;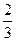 am-1,
am-1,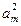 ,am+1+
,am+1+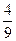 依次成等差数列.
依次成等差数列.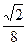 是等比数列4
是等比数列4 ,4,2
,4,2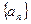 和
和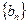 满足:
满足: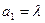 ,
,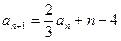 ,
,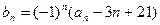 ,其中
,其中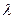 为实数,
为实数,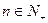 .
. 的等比数列
的等比数列 的前n项和为
的前n项和为 ,若
,若 、
、 成等差数列,则
成等差数列,则 ▲ .
▲ .