题目内容
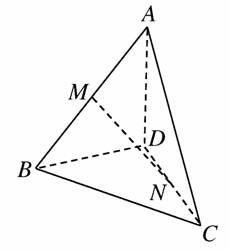
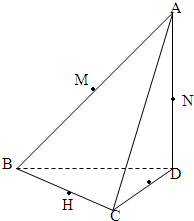 如图所示,已知三棱锥A-BCD中,AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点.
如图所示,已知三棱锥A-BCD中,AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点.(1)求证M、N、G、H四点共面;
(2)已知DC=1,CB=
| 2 |
| 6 |
分析:(1)根据两条平行线可以确定一个平面证明M、N、G、H四点共面,根据中位线证明直线平行.
(2)先证BC⊥平面ACD,在Rt△BCD中求出BD,在Rt△ABD用勾股定理求出球的半径,即可求球M的体积V
(2)先证BC⊥平面ACD,在Rt△BCD中求出BD,在Rt△ABD用勾股定理求出球的半径,即可求球M的体积V
解答:解(1)连接MH,NG,∵M、N、G、H分别是棱AB、AD、DC、CB的中点,
∴MH∥AC,NG∥AC,∴MH∥NG,根据两条平行线可以确定一个平面,∴∵M、N、G、H四点共面.
(2)设球半径为R,∵AB是球M大圆直径,点c在球面上,
∴MA=MB=MC=R,且∠ACB=90°,∴BC⊥AC,
∵AD⊥平面BCD,∴AD⊥BC,∵AC∩AD=A,∴BC⊥平面ACD,
∴BC⊥CD,∴BD2=BC2+CD2=3,
∵AD=
,∴AB2=3+6=9,
∴AB=3,∴球半径=
,
∴球体积V=
π.
∴MH∥AC,NG∥AC,∴MH∥NG,根据两条平行线可以确定一个平面,∴∵M、N、G、H四点共面.
(2)设球半径为R,∵AB是球M大圆直径,点c在球面上,
∴MA=MB=MC=R,且∠ACB=90°,∴BC⊥AC,
∵AD⊥平面BCD,∴AD⊥BC,∵AC∩AD=A,∴BC⊥平面ACD,
∴BC⊥CD,∴BD2=BC2+CD2=3,
∵AD=
| 6 |
∴AB=3,∴球半径=
| 3 |
| 2 |
∴球体积V=
| 9 |
| 2 |
点评:本题用到公理两条平行线可以确定一个平面,线面垂直的判定定理,勾股定理等知识点,训练学生分析问题,解决问题的能力.

练习册系列答案
相关题目
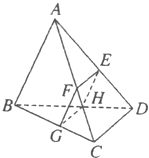 如图所示,已知三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证:
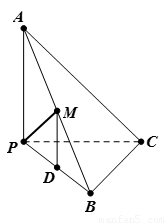
如图所示,已知三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证: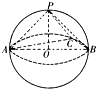 如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,
如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,