题目内容
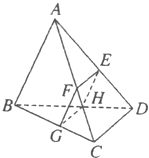 如图所示,已知三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证:
如图所示,已知三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证:(1)EF∥平面BCD;
(2)EF∥CD;
(3)CD∥平面EFGH.
分析:(1)由于EFGH为平行四边形,可得EF∥GH. 再利用直线和平面平行的判定定理可得 EF∥平面BCD.
(2)由(1)可得EF∥平面BCD,根据直线和平面平行的性质定理可得EF∥CD.
(3)由(2)可得EF∥CD,再根据直线和平面平行的判定定理可得 CD∥平面EFGH.
(2)由(1)可得EF∥平面BCD,根据直线和平面平行的性质定理可得EF∥CD.
(3)由(2)可得EF∥CD,再根据直线和平面平行的判定定理可得 CD∥平面EFGH.
解答:解:(1)证明:由于EFGH为平行四边形,∴EF∥GH.
由于GH?平面BCD中,EF不在平面BCD中,故有EF∥平面BCD.
(2)由(1)可得EF∥平面BCD,而EF?平面ACD,平面ACD∩平面BCD=CD,根据直线和平面平行的性质定理可得EF∥CD.
(3)由(2)可得EF∥CD,EF?平面EFGH,CD不在平面 EFGH内,故有CD∥平面EFGH.
由于GH?平面BCD中,EF不在平面BCD中,故有EF∥平面BCD.
(2)由(1)可得EF∥平面BCD,而EF?平面ACD,平面ACD∩平面BCD=CD,根据直线和平面平行的性质定理可得EF∥CD.
(3)由(2)可得EF∥CD,EF?平面EFGH,CD不在平面 EFGH内,故有CD∥平面EFGH.
点评:本题主要考查直线和平面平行的判定定理、性质定理的应用,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
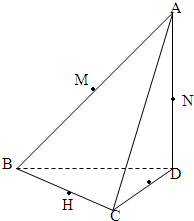 如图所示,已知三棱锥A-BCD中,AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点.
如图所示,已知三棱锥A-BCD中,AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点.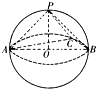 如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,
如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,